|
ریاضیات | ||
|
1. اعداد مختلط
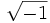 را را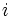 مینامیم، در این صورت تمام اعداد منفی با معنی خواهد بود، در نتیجه معادلههای درجه دوم، همگی ریشه های با معنی ای خواهند داشت برای مثال مینامیم، در این صورت تمام اعداد منفی با معنی خواهد بود، در نتیجه معادلههای درجه دوم، همگی ریشه های با معنی ای خواهند داشت برای مثال 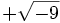 و و  ، یا در واقع ، یا در واقع  ، ریشه های معادله ، ریشه های معادله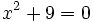 هستند. اما این گونه اعداد، حقیقی نیستند، چراکه مجذور آنها مثبت نیست. بنابراین با اعداد جدیدی روبرو هستیم. این اعداد را اعداد مختلط ( یا موهومی ) نامیده اند. هستند. اما این گونه اعداد، حقیقی نیستند، چراکه مجذور آنها مثبت نیست. بنابراین با اعداد جدیدی روبرو هستیم. این اعداد را اعداد مختلط ( یا موهومی ) نامیده اند. نماد 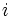 ، اولین بار توسط اویلر در قرن هیچدهم معرفی شده است و برابر است با ، اولین بار توسط اویلر در قرن هیچدهم معرفی شده است و برابر است با 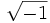 . بدین ترتیب به ازای اعداد حقیقی . بدین ترتیب به ازای اعداد حقیقی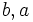 ، عدد ، عدد 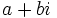 ، عددی مختلط است که به ، عددی مختلط است که به 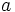 بخش حقیقی و به بخش حقیقی و به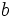 بخش مختلط گفته میشود. اگر بخش مختلط گفته میشود. اگر 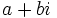 بنامیم،مینویسیم : بنامیم،مینویسیم : 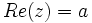 و و 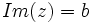 ، که ، که 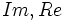 بترتیب معرف بخش حقیقی و مختلط هستند. بترتیب معرف بخش حقیقی و مختلط هستند. حال اگر اعداد مختلط 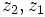 را چنین تعریف کنیم: را چنین تعریف کنیم: 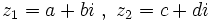 حاصل جمع و حاصل ضرب آن ها این گونه تعریف میشود 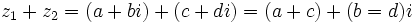 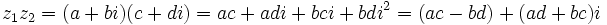 زیرا همان طور که گفتیم، 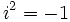 میباشد. میباشد. بنابراین جمع و ضرب اعداد مختلط دارای خواص زیر است: 1.جابجایی: 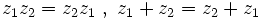 . . 2.شرکت پذیری: 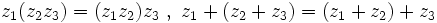 . . 3.توزیع پذیری ضرب نسبت به جمع: 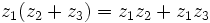 صفر مختلط برابر است با 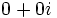 ، همچنین ، همچنین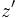 را قرینه را قرینه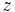 نامیم هر گاه: نامیم هر گاه: 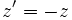 . . 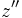 را معکوس را معکوس 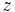 گوییم هر گاه: گوییم هر گاه: 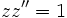 ، بدین ترتیب: ، بدین ترتیب: 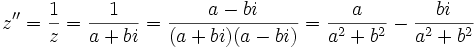 در نتیجه حاصل تقسیم 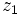 بر بر 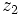 چنین محاسبه میشود: چنین محاسبه میشود: 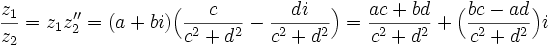 و یک نوع نمایش نیز به این شکل است: 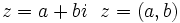 . . بنابراین اگر فرض کنید 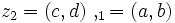 نقاطی در صفحه اند، داریم: نقاطی در صفحه اند، داریم: 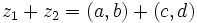 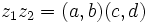 که جمع و ضرب آن ها بنابر آنچه که تعریف کردیم، چنین خواهد بود: 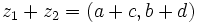 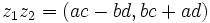 توجه کنید که هر عدد مختلط توسط 2 جزء 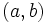 قابل نمایش است پس با این اعمال روی قابل نمایش است پس با این اعمال روی 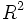 دستگاهی از اعداد پدید می آید که به آن دستگاه اعداد مختلط گویند، و آن را با دستگاهی از اعداد پدید می آید که به آن دستگاه اعداد مختلط گویند، و آن را با 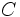 نمایش میدهند. صفحه ای که نقاط آن را اعداد مختلط تشکیل دهند، صفحه مختلط مینامند. این صفحه دارای دو محور افقی و عمودی است. تمام اعداد مختلطی را در نظر بگیرید ( مانند نمایش میدهند. صفحه ای که نقاط آن را اعداد مختلط تشکیل دهند، صفحه مختلط مینامند. این صفحه دارای دو محور افقی و عمودی است. تمام اعداد مختلطی را در نظر بگیرید ( مانند 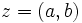 ) که بخش مختلط آن صفر است، این اعداد به صورت ) که بخش مختلط آن صفر است، این اعداد به صورت 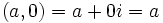 خواهند بود و همان طور که مشاهده می شود، اعدادی حقیقی هستند. یعنی محور افقی این صفحه، محور اعداد حقیقی است. حال اگر بخش حقیقی آن را صفر کنید، اعدادی به صورت 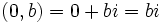 بدست می آیند، که محور عمودی این صفحه را تشکیل می دهند و به اعداد مختلط محض معروفند. بدست می آیند، که محور عمودی این صفحه را تشکیل می دهند و به اعداد مختلط محض معروفند. با این تعاریف داریم: 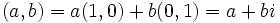 و آنچه که در مورد جمع و ضرب اعداد مختلط تعریف نمودیم بر تعریف آن در صفحه مختلط هم منطبق خواهد بود. لذا نمایش عدد مختلط 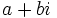 در صفحه مختلط همان نمایش زوج مرتب در صفحه مختلط همان نمایش زوج مرتب 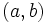 خواهد بود: خواهد بود: 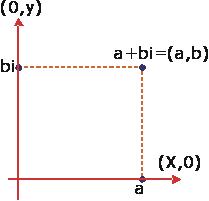
[ جمعه 92/2/20 ] [ 6:47 صبح ] [ محمد رضا جبین پور ]
[ نظرات () ]
|
||
| [قالب وبلاگ : سیب تم] [Weblog Themes By : SibTheme.com] | ||
