
|
ریاضیات | ||
|
تعریف
· لازم به ذکر است زاویه ها را با وسیله ای به نامنقاله اندازه گیری می کنند که بر حسب درجه مقیاس بندی شده اند. واحد های اندازه گیری زاویه: · درجه: اگر محیط یک دایره دلخواه را به 360 قسمت مساوی تقسیمکنیم هر قسمت را یک درجه می نامند. به عبارت دیگر یک درجه یک سیصد و شستم محیط یکدایره است.
· استفاده از واحد درجه(degree) برای اندازه گیریزاویه به بابلی ها منسوب است که با دستگاه اعداد در مبنای 60 کار می کردند. همچنین 360 درجه احتمالا از تعداد روزهای سال بابلی ها نشات گرفته است سالی که دارای 12ماه 30روزه است. اجزایدرجه:
[ چهارشنبه 92/3/1 ] [ 6:46 صبح ] [ محمد رضا جبین پور ]
[ نظرات () ]
3.6 میلیارد سال نوری: فاصله زمین از یک انفجار پرتو گامای به تازگی کشف شده که درخشانترین انفجار مشاهده شده توسط دانشمندان ناسا تاکنون به شمار میرود. 25 هزار دلار: جریمه اینترنتی که ارائهکنندگان اینترنت در صورت عدم جاسوسی برای پلیس فدرال آمریکا باید بصورت روزانه پرداخت کنند. 200 اسببخار: قدرت موتور توربو دیزل هواپیمای مسافربری چهار نفره Synergy که یکی از بزرگترین اختراعات سال است. 1042: تعداد سنگهای فضایی که بشرتا کنون فرود آنها را بر زمین شاهده بوده است. 750 میلیون دلار: قیمت بلیت سفر به مریخ در فرودگر ماه پامپکین 120: تعداد دفعاتی که بالهای کوچکترین ربات پرنده جهان به هم میخورد. 2: تعداد جرائمی که یک دختر نوجوان پس از ایجاد یک انفجار تصادفی در آزمایشگاه علمی مدرسه خود با آن روبرو شد. 2019: سالی که به گفته باز آلدرین، دومین انسانی که بر ماه فرود آمد، رئیسجمهور آمریکا باید برای اعزام انسان به مریخ متعهد شود. 37 میلیارد دلار: مبلغی که نیروی دریایی آمریکا برای ساخت ناوجنگی کشتی رزمی ساحلی خرج کرده که به ندرت کار میکند. 2 سال: طول زمانی که آزمایشگاه ملی لوسآلموس از اینترنت کوانتومی مخفیانه برخوردار بوده است. 1937: سالی که بالون هایندنبرگ زپلین بر فراز نیوجرسی منفجر شده و منجر به کشته شدن 35 تن و پایان ناگهانی عصر بالونسواری شد. 2.62 میلیون سال: نیمی از عمر آهن-60، یکی ایزوتوپ سنگین آهن است که اخیرا درون باکتری 2.2 میلیون ساله در کف دریا کشف شدهاست. 20: تعداد سرنگهای حاوی خاک ماه ماموریت آپولو 11 که اخیرا پس از یک دوره چند ساله که در انبار گم شده بود، پیدا شد. 250 دلار: قیمت تبلت اندروید جدید شرکت e-ink موسوم به «ارل» که برای استفاده در حیات وحش طراحی شده است. 33 کیلوهرتز: حد نهایی فرکانس صوت که توسط شبپره بزرگ موم، حشرهای که از بالاترین حد شنوایی در زمین برخوردار بوده، قابل شنود است. 1 روز: طول زمانی که ساخت یک هاب یواسبی DIY برای نصب روی دوچرخه و شارژ کردن دستگاههای الکتریکی در زمان حرکت وقت میبرد. 200 مایل بر ساعت: نهایت سرعت خودروی پرنده ترافوجیا TF-Xبا قابلیت برخاست عمودی و فرود خودکار 30 دلار: هزینه یک موتور مقوایی 13 کیلوگرمی آلفا که میتواند راننده تا 20 برابر وزن خود را حمل کند. [ دوشنبه 92/2/30 ] [ 6:17 صبح ] [ محمد رضا جبین پور ]
[ نظرات () ]
نام بازی : Symmetry Artist هدف بازی : بازی برای آموزش رسم تقارن نسبت به محور های مختلف ،نقاط مختلف و ... نحوه بازی :محور یا نقطه ای که میخواهید نسبت به آن تقارن را رسم کنید ، انتخاب کرده شکل مورد نظرتان را با مداد رسم کنید خود به خود تقارن شکل رسم می شود . راهنمای اجرای بازی : اجرای این بازی ها نیاز به نصب flash player دارد  دانلود flash player دانلود flash player  شروع بازی شروع بازی [ شنبه 92/2/28 ] [ 6:37 صبح ] [ محمد رضا جبین پور ]
[ نظرات () ]
درایتالیا آثار کاوالیری فصل جدیدی در هندسه بوجود آورد. وی در سال 1629 ایدهآلهای ارشمیدس را تحت عنوان «هندسه غیر قابل تقسیمها» دنبال نمود و در 1635 نیز کتابی به همین نام انتشار داد. طبق نظر او هریک از اجزاء مرتباً تقسیم بدو میشدند و بینهایت کوچک میگردیدند. همچنین اولین جستجوهای مربوط بهحساب بینهایت کوچکها از اوست. [ جمعه 92/2/27 ] [ 6:16 صبح ] [ محمد رضا جبین پور ]
[ نظرات () ]
[ چهارشنبه 92/2/25 ] [ 11:39 صبح ] [ محمد رضا جبین پور ]
[ نظرات () ]
1- آیه قرآنی را ترجمه کنید سوره مزمل آیه 20 ( فَاقرئوا ماتَیَسَّرُ مِنَ القُرآن ).................. 2-صحیح یا غلط بودن موارد زیر را مشخص کنید . الف) بهترین راه برای انتخاب مرجع تقلید مشورت با اهل علم است. ص () غ ( ) ب) در برابر چشم دیگران و برای اینکه از او تعریف کنند وضو می گیرد. ص () غ () ج) وضو گرفتن با هر آبی صحیح است . ص () غ () د) یکی از دلایل برای بلاها این است که ما را به شایستگی برساند . ص () غ () 3-مناسب ترین جواب را با علامت مشخص کنید . 1-درکدام مورد وضو گرفتن واجب است ؟ الف) رفتن به مسجد () ب : زیارت اهل قبور () ج : هنگام تلاوت قرآن () د : دست زدن به یکی از نامهای خداوند () 2- از مبطلات نماز است . الف : روی برگرداندن از قبله () ب: پاک بودن اعضای وضو () ج: پاک بودن آب وضو () د: فرو بردن زره های ریز غذا () 4-جای خالی را با کلمات مناسب پر کنید . الف : خداوند بخشایشگر نه تنها خطاهای کوچک بلکه همه ی .... را نیز می آمرزد . ب: یوم الفصل یعنی .......................... . 5-به سوالات پاسخ کوتاه دهید . الف : غفّار یعنی ................................... ب : یوم الحساب یعنی .......................... 6-موارد ستون الف را به ستون ب وصل کنید . الف ب 1 : یکی از مواردی که باید گذشت کرد 1 : مرجع تقلید 2 : اگر اعضای وضو نجس باشد وضو .... 2: به اشتباهش پی برده باشد 3: پیام های اصلی همه رسولان ....... 3: باطل 4: برای یادگیری از احکام به او مراجعه می کنیم 4: یکسان بود 7-به سوال پاسخ کامل دهید . کدام نماز تاثیر عمیقی بر خوشبختی انسان و خوشنودی خداوند خواهد گذاشت ؟ 8-حضرت علی (ع) درباره ویژگیهای قرآن چه می فرمایند؟ 9-سه مورد از شرایط مرجع تقلید را بیان کنید 10-دو مورد از مواردی که مکلف باید برای نماز تیمم کند بیان کنید . 11- چرا روز آغاز تکلیف را باید جشن گرفت ؟ 12- باقیات الصالحات یعنی چه ؟ [ سه شنبه 92/2/24 ] [ 6:36 صبح ] [ محمد رضا جبین پور ]
[ نظرات () ]
[ دوشنبه 92/2/23 ] [ 3:13 عصر ] [ محمد رضا جبین پور ]
[ نظرات () ]
قرن هفدهم در تاریخ ریاضیات قرنی عجیب و معجزهآسا است. از فعالترین دانشمندان این قرن کشیشی پاریسی بود بنام مارن مرسن که میتوان وی را گرانبهاترین قاصد علمی جهان دانست. این شخص اطلاعات لازم را به دانشمندان میداد و به ملاقات ایشان میرفت و هر هفته آنان را در کلبه خود جمع میکرد و وسیله تبادل افکارشان را فراهم میساخت. و حتی برای اینکه بتواند آثار علمای مزبور را منتشر کند، شخصاً چاپخانهای تهیه کرد و رابط مابین گالیله،دکارت،فرما و دیگران شد. به مدد همین اجتماعات بود که کولیر توانست آکادمی علوم پاریس را در سال 1666 تأسیس کند.
در سال 1609گالیله ریاضیات و نجوم را در دانشگاه پادوا در ایتالیا تدریس میکرد. وی یکی از واضعین مکتب تجربی است. مخالفت او با اصول ارسطو اشکالات بزرگی برای وی تولید کرد و میدانیم که در سال 1663 وی در سن هفتاد سالگی در برابر دادگاه تفتیش عقاید حاضر شد و چون بعد از کوپرینک اول کسی بود که حرکت زمین را به دور خورشید تأیید کرد محکوم گردید. وی قانون سقوط اجسام را به دست آورد و مفهوم شتاب را تعریف کرد و آن عبارت است از ازدیاد سرعت در هر ثانیه و همچنین قوانین حرکت گلوله روی سطح افقی و سطح شیبدار نیز مطالعه نمود. گالیله موفق به اختراع دوربینی گردید که هنوز هم نام او را همراه دارد. در همان اوقات که گالیله نخستین دوربین خود را به سوی آسمان متوجه نمود در 31 مارس 1596در تورن فرانسه رنه دکارت بدنیا آمد. وی به زودی با مارن مرسسن که یکی از همکلاساش بود دوست شد و پس از یکدوره فعالیتهای نظامی و مسافرتهای متعدد به پاریس و هلنددر سال 1650 درسوئد زندگی را بدرود گفت. دکارت در میان همه کارهایش از عرضه نمودن افکار فلسفی خود در روابط بین انسان و طبیعت غفلت ننمود. کتاب وی به نام دیوپتریک که موضوع آن مسائل مربوط به مبحث نور بویژه انکسار میباشد جزو برجستهترین آثار اوست. نام ریاضیدان بزرگ سوئیسی «پول گولدن» را نیز باید با نهایت افتخار ذکر کرد. شهرت وی بخصوص بواسطه قضایای مربوط به اجسام دوار است که نام او را دارا میباشد و در کتابی به نام «مرکز ثقل» ذکر شده است. دیگر از دانشمندان برجسته قرن هفدهم پییردوفرما ریاضیدان بزرگ فرانسوی است که در سال 1601 در بومون دوکانی متولد شد و در 1665 در کاستر درگذشت. وی مطالعات عمیق و جالبی درباره ریاضیات مطلق و نور کرد. یکی از برجستهترین آثار او «تئوری اعداد» است که وی کاملاً بوجود آورنده آن میباشد. در هندسه، فرما در همان زمان دکارت و مستقل از او مبانی هندسه تحلیلی را کشف کرد، گذشته از آن وی از دکارت نیز تجاوز نمود و اولین کسی است که این علم را در مورد فضای سه بعدی بکار برد. تجسمات رفیع و استادانه او در حساب عالی است تا جائی که استدلال بعضی از قضایای او فقط یک قرن بعد بوسیله کسانی از قبیل اولرولاگرانژ باز یافته شد و یکی از قضایای او را حتی امروز نیز نتوانستهاند ثابت کنند. ریاضیدان بزرگ دیگری که در این قرن به خوبی درخشید ژیرار دزارک فرانسوی میباشد که بیشتر به واسطه کارهای درخشانش در هنر معماری شهرت یافته بود. دزارک در هندسه آثاری ارزشمند دارد ومیتوان گفت که وی راه به سوی آنچه که «هندسه جدید» نامیده میشود بازکرد. او نخستین کسی است که درباره اشکال هندسی تنها به روابط متری مابین کمیات اکتفا نکرد و خواص تصویری را نیز در نظر گرفت و هندسه وضعی را پدید آورد. و بالاخره ریاضیدان دیگر فرانسوی یعنی روبروال را باید نام ببریم که بواسطه ترازوی مشهوری که نام او را همراه دارد همه جا معروف است. در اواسط قرن هفدهم کمکم مقدمات اولیه آنالیز عناصر بینهایت کوچک در تاریکی و ابهام بوجود آمد و رفتهرفته سر و صدای آن به گوش مردم رسید و فکرها را بدان سوی متوجه ساخت. این نکته را نیز بایستی متذکر شد که مرکز ثقل علمی اروپا تغییر کرده بود:ایتالیا که مدتهای مدید درخشیده بود کمکم به خاموشی میگرائید. آلمان بلافاصله بعد از کپلر دچار جنگهای سی ساله شد و دیگر تا هنگام درخشیدن لایب نیتس گفتگوئی از آن در میان نبود.انگلستاندر انتظار پیدایش موجود مافوق بشری همچون نیوتن بود و کشور هلند به انتظار هویگنس تنها به تربیت مردان علاقمند و متبحر اکتفا میکرد. در این احوال کشور فرانسه اولین مقام علمی را اشغال کرده بود. کدام کشور میتوانست مدعی وجود کسانی همچون دکارت،فرما، دزارک ، روبروال و پاسکال باشد. بدون شک پاسکال همراه با دکارت و فرما یکی از سه ریاضیدان بزرگ نیمه اول قرن هفدهم بود و نیز میتوان ارزش او را در علم فیزیک برابر گالیله دانست. او هنگامی که هنوز آنقدر کم سن بود که خط راست را میله و دایره را گردی مینامید بدون آنکه هرگز کتاب هندسهای دیده باشد بسیاری از احکام سی و دو قضیه اولیه اقلیدس را خود به خود کشف کرده بود. درسن شانزده سالگی کتابی درباره مقاطع مخروطی نوشت و هنوز یکی از قضایای آن به نام او مشهور است، همچنین در هیجده سالگی یعنی در سال 1641 نخستین ماشینحسابرا اختراع کرد که هنوز در کنسرواتوار صنایع و مشاغل محفوظ است. [ شنبه 92/2/21 ] [ 6:35 صبح ] [ محمد رضا جبین پور ]
[ نظرات () ]
1. اعداد مختلط
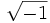 را را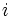 مینامیم، در این صورت تمام اعداد منفی با معنی خواهد بود، در نتیجه معادلههای درجه دوم، همگی ریشه های با معنی ای خواهند داشت برای مثال مینامیم، در این صورت تمام اعداد منفی با معنی خواهد بود، در نتیجه معادلههای درجه دوم، همگی ریشه های با معنی ای خواهند داشت برای مثال 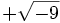 و و  ، یا در واقع ، یا در واقع  ، ریشه های معادله ، ریشه های معادله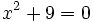 هستند. اما این گونه اعداد، حقیقی نیستند، چراکه مجذور آنها مثبت نیست. بنابراین با اعداد جدیدی روبرو هستیم. این اعداد را اعداد مختلط ( یا موهومی ) نامیده اند. هستند. اما این گونه اعداد، حقیقی نیستند، چراکه مجذور آنها مثبت نیست. بنابراین با اعداد جدیدی روبرو هستیم. این اعداد را اعداد مختلط ( یا موهومی ) نامیده اند. نماد 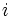 ، اولین بار توسط اویلر در قرن هیچدهم معرفی شده است و برابر است با ، اولین بار توسط اویلر در قرن هیچدهم معرفی شده است و برابر است با 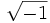 . بدین ترتیب به ازای اعداد حقیقی . بدین ترتیب به ازای اعداد حقیقی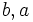 ، عدد ، عدد 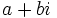 ، عددی مختلط است که به ، عددی مختلط است که به 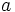 بخش حقیقی و به بخش حقیقی و به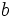 بخش مختلط گفته میشود. اگر بخش مختلط گفته میشود. اگر 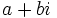 بنامیم،مینویسیم : بنامیم،مینویسیم : 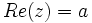 و و 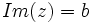 ، که ، که 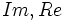 بترتیب معرف بخش حقیقی و مختلط هستند. بترتیب معرف بخش حقیقی و مختلط هستند. حال اگر اعداد مختلط 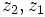 را چنین تعریف کنیم: را چنین تعریف کنیم: 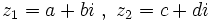 حاصل جمع و حاصل ضرب آن ها این گونه تعریف میشود 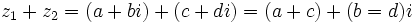 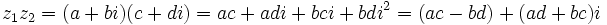 زیرا همان طور که گفتیم، 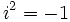 میباشد. میباشد. بنابراین جمع و ضرب اعداد مختلط دارای خواص زیر است: 1.جابجایی: 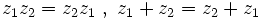 . . 2.شرکت پذیری: 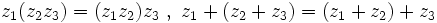 . . 3.توزیع پذیری ضرب نسبت به جمع: 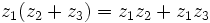 صفر مختلط برابر است با 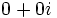 ، همچنین ، همچنین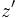 را قرینه را قرینه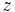 نامیم هر گاه: نامیم هر گاه: 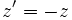 . . 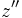 را معکوس را معکوس 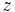 گوییم هر گاه: گوییم هر گاه: 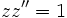 ، بدین ترتیب: ، بدین ترتیب: 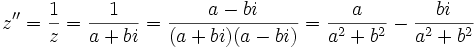 در نتیجه حاصل تقسیم 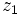 بر بر 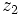 چنین محاسبه میشود: چنین محاسبه میشود: 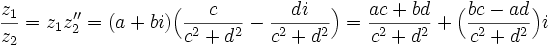 و یک نوع نمایش نیز به این شکل است: 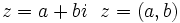 . . بنابراین اگر فرض کنید 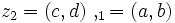 نقاطی در صفحه اند، داریم: نقاطی در صفحه اند، داریم: 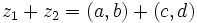 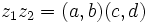 که جمع و ضرب آن ها بنابر آنچه که تعریف کردیم، چنین خواهد بود: 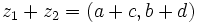 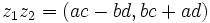 توجه کنید که هر عدد مختلط توسط 2 جزء 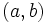 قابل نمایش است پس با این اعمال روی قابل نمایش است پس با این اعمال روی 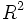 دستگاهی از اعداد پدید می آید که به آن دستگاه اعداد مختلط گویند، و آن را با دستگاهی از اعداد پدید می آید که به آن دستگاه اعداد مختلط گویند، و آن را با 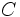 نمایش میدهند. صفحه ای که نقاط آن را اعداد مختلط تشکیل دهند، صفحه مختلط مینامند. این صفحه دارای دو محور افقی و عمودی است. تمام اعداد مختلطی را در نظر بگیرید ( مانند نمایش میدهند. صفحه ای که نقاط آن را اعداد مختلط تشکیل دهند، صفحه مختلط مینامند. این صفحه دارای دو محور افقی و عمودی است. تمام اعداد مختلطی را در نظر بگیرید ( مانند 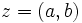 ) که بخش مختلط آن صفر است، این اعداد به صورت ) که بخش مختلط آن صفر است، این اعداد به صورت 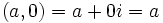 خواهند بود و همان طور که مشاهده می شود، اعدادی حقیقی هستند. یعنی محور افقی این صفحه، محور اعداد حقیقی است. حال اگر بخش حقیقی آن را صفر کنید، اعدادی به صورت 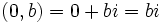 بدست می آیند، که محور عمودی این صفحه را تشکیل می دهند و به اعداد مختلط محض معروفند. بدست می آیند، که محور عمودی این صفحه را تشکیل می دهند و به اعداد مختلط محض معروفند. با این تعاریف داریم: 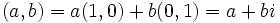 و آنچه که در مورد جمع و ضرب اعداد مختلط تعریف نمودیم بر تعریف آن در صفحه مختلط هم منطبق خواهد بود. لذا نمایش عدد مختلط 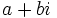 در صفحه مختلط همان نمایش زوج مرتب در صفحه مختلط همان نمایش زوج مرتب 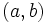 خواهد بود: خواهد بود: 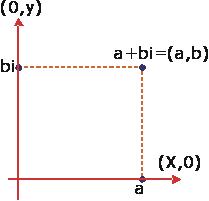
[ جمعه 92/2/20 ] [ 6:47 صبح ] [ محمد رضا جبین پور ]
[ نظرات () ]
[ چهارشنبه 92/2/18 ] [ 1:11 عصر ] [ محمد رضا جبین پور ]
[ نظرات () ]
|
||
| [قالب وبلاگ : سیب تم] [Weblog Themes By : SibTheme.com] | ||