|
ریاضیات 
| |||||||||||
|
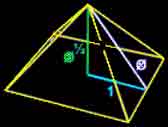
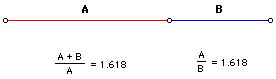
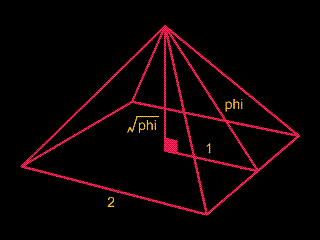
استفاده از عدد طلائی در معماری از قرن ها پیش آغاز شد.قدیمی ترین بنایی که در آن از نسبت طلائی استفاده شده است در طراحی اهرام مصر بوده است.
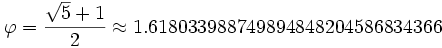
تعریف
کاربردها
عدد طلائی از دیدگاه کپلرکپلر (Johannes Kepler 1571-1630) منجم معروف نیز علاقه بسیاری به نسبت طلایی داشت بگونه ای که در یکی از کتابهای خود اینگونه نوشت : "هندسه دارای دو گنج بسیار با اهمیت می باشد که یکی از آنها قضیه فیثاغورث و دومی رابطه تقسیم یک پاره خط با نسبت طلایی می باشد. اولین گنج را می توان به طلا و دومی را به جواهر تشبیه کرد". [ جمعه 92/3/17 ] [ 6:46 صبح ] [ محمد رضا جبین پور ]
[ نظرات () ]
نام بازی : Decention هدف بازی : بازی برای اموزش برابری درصد ، کسر و اعشار نحوه بازی : در هر دایره باید عددی که کسر، درصد و اعشارش برابر است قرار دهید . راهنمای اجرای بازی : اجرای این بازی ها نیاز به نصب flash player دارد  دانلود flash player  شروع بازی [ چهارشنبه 92/3/15 ] [ 9:25 صبح ] [ محمد رضا جبین پور ]
[ نظرات () ]
تبدیل واحد های اندازه گیری زاویه به یکدیگر : فرض کنید اندازه زاویه 2- 3- از تساوی های فوق نتیجه می شود:
بهعنوان مثال اگر اندازه زاویه ای برابر 20 گراد باشد اندازه این زاویه بر حسب درجه ورادیان به این صورت محاسبه میشود:
· هر رادیان تقریبا برابر است با 57.3 درجهاست.
[ دوشنبه 92/3/13 ] [ 6:53 صبح ] [ محمد رضا جبین پور ]
[ نظرات () ]
ریاضیدانان انگلیسی سنسن و استوارت ضمن اکتشافات خود مسائل مختلفی از هندسه را استادانه مورد مطالعه قرار دادند. همچنین بروک تایلور و کولین ماکلرین کوششهای رها شدة اسحاق نیوتن را ادامه دادند. تایلور باعث توسعة فوق‌العادة آنالیز ریاضی عناصر بی‌نهایت کوچک که توسط لایب نیتس عرضه شده بود گردید و ماکلرین روش او را اصلاح کرد. [ یکشنبه 92/3/12 ] [ 6:26 صبح ] [ محمد رضا جبین پور ]
[ نظرات () ]
بازی مکعب هوش یک بازی فکری و تمرکزی جالب و نسبتاً دشوار که مطمئناً شما را جذب خود خواهد کرد. 
[ جمعه 92/3/10 ] [ 5:58 صبح ] [ محمد رضا جبین پور ]
[ نظرات () ]
· رادیان دایره ای به شعاع L را در نظر بگیرید. می دانیم محیطاین دایره
برای نمایش رادیان ازنماد«rad» استفاده می کنیم. بنابراین محیط هر دایره برحسب رادیان
به عنوان مثالمی خواهیم بدانیم اندازه زاویه مرکزی مقابل به کمانی از دایره که طول آن کمان · لازم به توضیح است که پر کاربرد ترین واحد اندازهگیری زاویه رادیان است که بویژه در مثلثات، حساب، فیزیک کاربرد فراوان دارد. [ چهارشنبه 92/3/8 ] [ 6:8 صبح ] [ محمد رضا جبین پور ]
[ نظرات () ]
 ارسطو در سال 384 ق. م، در استاگیرا واقع در شمال یونان چشم به جهان گشود. پدرش نیکو ماخوس، پزشک دربار پادشاه مقدونیه بود. [ سه شنبه 92/3/7 ] [ 6:32 صبح ] [ محمد رضا جبین پور ]
[ نظرات () ]
· گراد اگر محیط یک دایره را به 400 قسمت مساوی تقسیم کنیم هرقسمت را یک گراد می گویند. به عبارت دیگر یک چهارصدم دوران کامل، زاویه ای بهاندازه یک گراد پدید می آورد.گراد گاهی گون نیز گفته می شود. برای نمایش گراد ازنماد «gr» استفاده می شود. لذا می توان گفت:
پس بهاین ترتیب در این مقیاس اندازه زاویه تمام صفحه یا یک دور کامل 400 گراد و اندازهزاویه نیم صفحه برابر 200 گراد خواهد بود.
بهعنوان مثال اگر اندازه زاویه ای 37 گراد و 2 دسی گراد و 8 میلی گرا باشد مینویسیم: استفاده از این واحد برای زاویه در ریاضیات بسیار کم است. [ یکشنبه 92/3/5 ] [ 6:27 صبح ] [ محمد رضا جبین پور ]
[ نظرات () ]
[ جمعه 92/3/3 ] [ 6:13 صبح ] [ محمد رضا جبین پور ]
[ نظرات () ]
 تا بر شد از نیام فلق برق خنجرش برچید شب ز دشت و دمن، تیغ چادرش بر تارک ستیغ بر آمد شعاع صبح چونان پر خروس ز سیمینه مغفرش موجى بر آمد از ز بر کوه زرفشان پاشید بر کران افق زرّ احمرش جیب افق، زرنگ شفق لاله گونه شد بر آن نثار آمده بس درّ و گوهرش نقّاش صنع از قلم زرنگار ریخت شنگرف سوده در خط دیباج اخضرش مشّاطه سحر به دو صد رنگ دلپذیر آراست باغ و راغ بدست فسونگرش پیک نسیم سر خوش و دلکش وزید و داشت داروى جان ز رائحه مشک و عنبرش آهسته پر کشید به آغوش شاخسار تا کودک شکوفه نلغزد ز بسترش وا کرد چشم نرگس شهلا به بوسهاى گلخنده زد ز عاطفت مهر پرورش خورشید کم کم از افق دشتهاى دور بر شد چنانکه کوه و دمن شد مسخّرش پرتو فشاند بر سر هر کاخ و کومهاى آفاق زنده گشت ز چهر منوّرش بر زد علم به پهنه گسترده زمین تسلیم شد کران به کران در برابرش تا بسترد ز روى زمین زنگ تیرگى صد آبشار نور فرو ریخت بر سرش تا چهر باختر برهد از ظلام شب قندیل آفتاب بر آمد ز خاورش ظلمت زدوده گشت ز سیماى روشنش دهشت ربوده گشت ز رخسار عنبرش آمد فراز مکّه و تا نقش کعبه دید انبوه زر فشانده به هر کوى و معبرش بیدار گشت مکّه، دیارى که سالها بد خفته و نبود به سر ذوق دیگرش بگشوده گشت پنجرهها یک بیک بصبح تا نور آفتاب بتابد به منظرش خلقى برون شد از در هر آشیانهاى هر کس به کار سازى رزق مقدّرش آن یک به کوى آمد و آن یک به کارگاه آن یک به ذوق آمد و آن یک به متجرش جمعى روان شدند سوى کعبه کز نیاز بوسند خاک پایگه آسمان فرش بد کعبه در میانه آن شهر یادگار از دوره خلیل و سماعیل و هاجرش با چار رکن مهم استاده سرفراز حصنى که هست قائمه هفت کشورش گوئى به انتظار کسى بود آن سراى تا آید و چو جان بنشاند به مصدرش ناگه در آن حریم مهین بانوئى کریم پیدا شد و کرامت پیدا ز منظرش او بانوئى ز جمله نکویان دهر بود نادیده چشم عالم از آن نکوترش حجب و وقار بود بر اندام زینتش قدس و عفاف بود به رخسار زیورش اندر قریش پاک زنى بود مردوار بو طالب بزرگ پسندیده شوهرش از خاندان هاشم و زدوده خلیل زیبنده بانوئى و برازنده همسرش مىخواست کردگار کزین خاندان پاک نخلى بر آورد شرف و مردمى برش مىخواست کردگار کزین زوج مهر زاد طفلى به عرصه آرد تابنده اخترش مىخواست کردگار کزین دودمان پاک مردى بپاى دارد چون کوه پیکرش مىخواست کردگار فرازنده مهترى کزان به روزگار نجویند بهترش مىخواست کردگار که میراث عدل و داد بخشد به داده خواهترین دادگسترش مىخواست کردگار ز دامان فاطمه زوجى براى فاطمه بانوى محشرش مىخواست کردگار یکى بحر گسترد تا موج خیزد از دل در خون شناورش مىخواست کردگار بر آرد برادرى آب آور برادر و غمخوار خواهرش مىخواست کردگار یکى خواهر آورد تا بر کشد به دوش لواى برادرش مىخواست کردگار که در دشت کربلا گلبوتهها ببیند و گلهاى پر پرش مىخواست کردگار یکى طرفه قهرمان تا جاودانه باشد یار پیمبرش بازو چو بر گشاید بر بازوى ستم بازوى او گشاید با روى چنبرش اندر مصاف کفر چو شمشیر برکشد بنیان کفر بر کند و عمر و عنترش و اندر بر جماعت مسکین و دردمند سیلاب اشک بارد از دیده ترش گاهى یتیم را بنوازد چونان پدر گاهى صغیر را به عطوفت چو مادرش زهرى به کام دشمن و شهدى بکام دوست کاین طرفه را بنام بخوانند حیدرش طفلى چنان که قافیه سازان روزگار واماندهاند در بر طبع سخنورش طفلى چنانکه دیده بینندگان ندید مانند او به عرصه محراب و منبرش طفلى چنانکه رایت اسلام از او بلند کوتاه دست ظلم ز عزم توانگرش توفنده همچو رعد به پیکار دشمنان لرزنده همچو بید به نزدیک داورش دستیش بهر کوشش و هنگامه و نبرد دستى پى حمایت مظلوم و مضطرش دستیش بهر بخشش و انفاق و التیام و ز بهر انتقام برون دست دیگرش دستیش بهر چاره و درمان دردمند دست دگر به قبضه شمشیر و خنجرش دستى به پایمردى از پافتادگان دستى به پاسدارى اسلام و دفترش دستیش بر پرستش و پیمان و پاس حق دستیش بر ستیزش بتخواه و بتگرش دستى بسوى خالق و دستى بسوى خلق دستى پى نوازش و دستى به کیفرش دستى بسوى تیره گردنکشان دراز دستى بسوى میثم و عمّار و بوذرش با این دو دست و بازوى مردانه دیگر کراست نام ید اللّه فراخورش چشمش بدان سراى که تا صاحب سراى آید به پیشباز و بخواند به محضرش آن روز میهمان خدا بود فاطمه یا للعجب که خانه فرو بسته بد درش او را ودیعهاى ز خدا بود در مشیم مىخواست تا ودیعه نهد در برابرش لختى به انتظار به گرد حرم گذشت سوزنده از شراره آزرم پیکرش ناگه ز سوى خانه یکى ایزدى خروش بنواخت گوش خلق ز مضراب تندرش پهلو شکافت خانه و شد معبرى پدید خانه خداى، فاطمه را خواند در برش و آنگه بهم بر آمد آن سهمگین شکاف آنسان که هیچ دیده نیارست باورش بعد از سه روز باز پدید آمد آن شکاف چونان صدف ز سینه بر او درّ گوهرش بنهاد گام فاطمه بیرون از آن سراى شادان ز میزبانى دادار اکبرش اندر مطاف خانه بدیدند جمله خلق طفلى چو ماهپاره در آغوش مادرش طفلى چنانکه مادر هستى نپرورد دیگر چو او به دایره مرد پرورش طفلى چنانکه خامه صورتگر خیال آنسان که نقش اوست نیارد مصوّرش خواهم مدیح گفتن فرزند کعبه را باشد که را مدیح ید اللّه میسرش آنرا که زیب قامت او «هل اتى» بود آنرا که هست افسر «لولاک» بر سرش آنرا که در مجاهدت و طاعت و سخى ایزد ستوده است به قرآن مکرّرش آنرا که گر نزاد همى مادر زمان هستى عقیم بود ز پورى دلاورش آنرا که تا نهال مساوات بر دهد آتش نهاد در کف اعمى برادرش من چون مدیح گویم آنرا که در نبرد مردان روزگار بخواندند صفدرش من چون مدیح گویم آنرا که در نماز بخشود بر فقیر نگین به آورش من چون مدیح گویم آنرا که مصطفى بگزید بهر فاطمه شایسته دخترش من چون مدیح گویم آن یکّه مرد را کز رزم بر نتافت عنان تک آورش من چون مدیح گویم آنرا که در غدیر بنشاند کردگار بجاى پیمبرش گویندگان سرودهاند بسیار جامهها از من چنان نیاید ستودن ایدرش من این سخن سرودم و شرمندهام ز خویش کز قطره کمترم بر پهناى کوثرش باشد که در شمار مرا توشه آورد یک ذره از غبار قدمهاى قنبرش گفتم من این قصیده به معیار آنکه گفت «صبح از حمایل سحر آهیخت خنجرش» حمید سبزواری [ پنج شنبه 92/3/2 ] [ 6:52 صبح ] [ محمد رضا جبین پور ]
[ نظرات () ]
|
درباره وبلاگ  در هر چیز از جمله یک نظریه ریاضی زیبایی را میتوان درک کرد اما نمی توان توضیح داد. | ||||||||||
| [قالب وبلاگ : سیب تم] [Weblog Themes By : SibTheme.com] | |||||||||||
