|
ریاضیات | |||
انتگرال
اَنتِگرال (integral) مقدار مشترک ممکن زیرین? مجموعهای ریمانی و زبرین? مجموعهای ریمانی یک تابع حقیقی در باز? مفروض است.[1] انتگرال از مفاهیم اساسی در ریاضیات است که در کنار مشتق دو عملگر اصلی حساب دیفرانسیل و انتگرال را تشکیل میدهند. نخستین بار لایب نیتس نماد استانداردی برای انتگرال معرفی کرد. 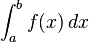
aو b نقاط ابتدا و انتهای بازه هستند و از لحاظ تاریخی
انتگرال نامعینتعریف:
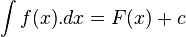

مثال: مقدار انتگرال تابع
انتگرال معینبنا به تعریف، نماد
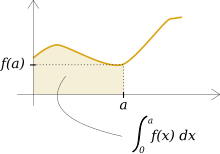
تابع انتگرالپذیراگر تابعی دارای انتگرال باشد به آن انتگرالپذیر گویند. تعبیر هندسی انتگرالاز نظر هندسی انتگرال برابر است با مساحت سطح محصور زیر نمودار.
مثالانتگرال یک تابع مثبت پیوسته در بازه (0,10) در واقع پیدا کردن مساحت محصور بین خطوط x=0 , x=10 و خم منحنی انتگرال یک تابع مساحت زیر نمودار آن تابع است. انتگرال گیری(محاسبه انتگرال) انتگرال گیری به معنی محاسبه سطح زیر نمودار با استفاده از روشها وقوانین انتگرال گیری است. مهمترین تعاریف در انتگرالاز مهمترین تعاریف در انتگرال میتوان از انتگرال ریمان و انتگرال لبگ است. انتگرال ریمان بهوسیله برنهارد ریمان در سال 1854 ارائه شد که تعریف دقیقی را از انتگرال ارائه میداد تعریف دیگر را هنری لبگ ارائه داد که طبق این تعریف شرایط تعویض پذیری حد و انتگرال با شرط مساوی ماندن عبارت، ارائه میکرد. از دیگر تعاریف ارائه شده در زمینه انتگرال میتوان به انتگرال ریمان–استیلتیس اشاره کرد. پس به طور خلاصه سه تعریف زیر از مهمترین تعاریف انتگرال میباشند: محاسبه انتگرالاکثر روشهای اساسی حل انتگرال بر پایه قضیه اساسی حساب دیفرانسیل و انتگرال بنا نهاده شده است که بر طبق آن داریم: 1.f تابعی در بازه (a,b) در نظر میگیریم. 2.پاد مشتق f را پیدا میکنیم که تابعی است مانند f که و داریم: 3.قضیه اساسی حساب دیفرانسیل و انتگرال را در نظر میگیریم: بنابراین مقدار انتگرال ما برابر خواهد بود. به این نکته توجه کنید که انتگرال واقعاً پاد مشتق نیست (یک عدد است) اما قضیه اساسی به ما اجازه میدهد تا از پاد مشتق برای محاسبه مقدار انتگرال استفاده کنیم. معمولاً پیدا کردن پاد مشتق تابع f کار سادهای نیست و نیاز به استفاده از تکنیکهای انتگرالگیری دارد این تکنیکها عبارتاند از :
روش هایی دیگر نیز وجود دارد که برای محاسبه انتگرالهای معین به کار میرود همچنین میتوان بعضی از انتگرالها با ترفند هایی حل کرد برای مثال میتوانید به انتگرال گاوسی مراجعه کنید. تقریب انتگرالهای معینمحاسبه سطح زیر نمودار بهوسیله مستطیل هایی زیر نمودار. هر چه قدرعرض مستطیلها کوچک میشوندمقدار دقیق تری از مقدار انتگرال بدست میآید.
کاربردانتگرالها در واقع مساحت محصور در زیر نمودار هستند و در فیزیک میتوان برای کاربردهای زیادی تعریف کرد مانند کار انجام شده در یک فر آیند ترمودینامیکی از انتگرال رابطه فشار و حجم به دست میآید. اما به طور کلی میتوان آن را تغییرات کمیت حاصل ضرب افقی و عممودی نمودار نامیدمثلا: در یک رابطه کمیتها را تحلیل ابعادی می کنیم مثلا رابطه سرعت و زمان را به صورت زیر نوشته میشود: سپس دو تحلیل را در هم ضرب می کنیم: پس مساحت محصور در زیر نمودار برابر با تغییرات طول (جابجایی) است. [ جمعه 92/2/6 ] [ 6:41 صبح ] [ محمد رضا جبین پور ]
[ نظرات () ]
|
|||
| [قالب وبلاگ : سیب تم] [Weblog Themes By : SibTheme.com] | |||
 تابعی انتگرالپذیر است و
تابعی انتگرالپذیر است و 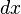 نمادی برای متغیر انتگرالگیری است.
نمادی برای متغیر انتگرالگیری است.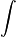 نمایش میدهند. به انتگرال نامعین ضد مشتق نیز گفته میشود, زیرا عمل انتگرال نامعین گرفتن دقیقا برعکس عملیات
نمایش میدهند. به انتگرال نامعین ضد مشتق نیز گفته میشود, زیرا عمل انتگرال نامعین گرفتن دقیقا برعکس عملیات 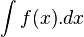 را انتگرال نامعین نامیده وحاصل آن را تابعی مانند
را انتگرال نامعین نامیده وحاصل آن را تابعی مانند  در نظر میگیریم هرگاه داشته باشیم:
در نظر میگیریم هرگاه داشته باشیم: را حساب کنید:
را حساب کنید: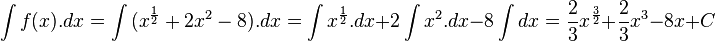

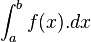 را انتگرال معین نامیده و حاصل آن را به ازای
را انتگرال معین نامیده و حاصل آن را به ازای  عددی به صورت زیر تعریف میکنیم:
عددی به صورت زیر تعریف میکنیم:
 و
و  به ترتیب، کرانهای بالا و پایین انتگرال نامیده میشوند.
به ترتیب، کرانهای بالا و پایین انتگرال نامیده میشوند. است. aو b نقاط ابتدا و انتهای بازه هستند و f تابعی انتگرالپذیر است و dx نمادی برای متغیر انتگرال گیری است.
است. aو b نقاط ابتدا و انتهای بازه هستند و f تابعی انتگرالپذیر است و dx نمادی برای متغیر انتگرال گیری است.

![v=[L]/[T] t=[T] \!](http://upload.wikimedia.org/math/8/2/2/822905b570a5c6ea0f79e5f228645e54.png)
![[L] \!](http://upload.wikimedia.org/math/b/2/6/b2600468c360b80f3b363f56c4ddd214.png)
