|
ریاضیات | ||||||||||||||||||||||||||||||||||
|
ویژگیهای قدر مطلق: برای هر عدد حقیقی a قدر مطلق a که آن را با |a| نمایش میدهیم به صورت زیر تعریف میشود: همان گونه که در بالا نشان داده شدهاست قدر مطلق یک عدد همواره صفر یا مثبت است و هرگز منفی نیست. در هندسه تحیلی قدر مطلق یک عدد حقیقی برابر است با فاصله آن تا صفر بر روی یک خط حقیقی؛ در حالت کلی قدر مطلق تفاضل دو عدد برابر است با فاصله? میان آن دو عدد. در واقع میتوان گفت که مفهوم تابع فاصله در ریاضی همان قدر مطلق تفاضل است که در حالت کلی بیان شدهاست. ریشه دوم یک عدد را میتوان به صورت زیر نشان داد: که گاهی از آن به عنوان تعریف قدر مطلق استفاده میشود. چهار ویژگی اصلی قدر مطلق عبارتند از:
دیگر ویژگیهای آن عبارتند از:
اگر فرض کنیم که b > 0 است آنگاه دو ویژگی دیگر قدر مطلق میتوان چنین نوشت: از این ویژگیها میتوان در حل نامساویها استفاده کرد؛ برای نمونه: از قدر مطلق دز تعیین فاصله مطلق در سامانه? متری در مجموعه اعداد حقیقی استفاده میشود. تابعهای قدر مطلقتابع حقیقی قدر مطلق در همه جا پیوسته است و در همه جا به جز نقطه? x = 0 مشتقپذیر است. این تابع در بازه? [0 ∞-) اکیدا نزولی و در بازه? (∞+ 0] اکیدا صعودی است و چون قدر مطلق عدد مثبت و منفی با هم برابر است پس تابعی زوج است و وارون ناپذیر. در تابع حقیقی قدر مطلق، تابع مرکب خود آن به صورت مشتق تابع قدر مطلقمشتق تابع قدر مطلق حقیقی برابر است با تابع علامت که با نماد sgn نمایش داده میشود، تابع زیر تنها به ازای xهای ناصفر تعریف شدهاست: تابع قدر مطلق حقیقی در x = 0 مشتقپذیر نیست. [ چهارشنبه 92/1/21 ] [ 6:44 صبح ] [ محمد رضا جبین پور ]
[ نظرات () ]
|
||||||||||||||||||||||||||||||||||
| [قالب وبلاگ : سیب تم] [Weblog Themes By : SibTheme.com] | ||||||||||||||||||||||||||||||||||











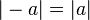


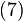







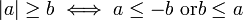



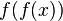 با خود تابع
با خود تابع 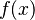 برابر است.
برابر است.

