|
ریاضیات | |||||||||||
|
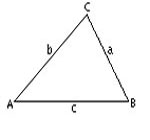
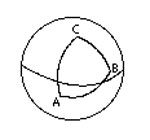
مثلث ار اساسی ترین اشکال در هندسه میباشد.یک مثلث دارای سه راس است که سه ضلع این رئوس را به هم وصل میکند.در هندسه اقلیدسی این اضلاع خطوطی مستقیم هستند. ولی در هندسه کروی این اضلاع کمان هایی از دایره عظیمه میباشند.این دو نوع مثلث را میتوانید در شکلهای روبرو مشاهده نمایید. انواع مثلث
|
|||||||||||
|
در این فرمول b طول قاعده و h طول ارتفاع مثلث میباشد. در شکل زیر نحوه بدست آمدن این فرمول بیان شده است:
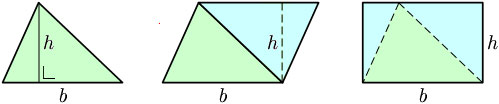 |
| تبدیل مثلث به یک متوازی الاضلاع که دو برابر مثلث مساحت دارد وسپس تبدیل متوازی الضلاع به یک مستطیل |
برای پیدا کردن مساحت مثلث (قسمت سبز) ابتدا یک کپی از مثلث (قسمت آبی) را برداشته و آن را 180 درجه میچرخانیم و به مثلث اولیه متصل میکنیم تا یک متوازی الاضلاع بدست آید. با بریدن قسمتی از متوازی الاضلاع و متصل کردن آن به ضلع دیگر آن(همانند شکل) یک مستطیل ایجاد میشود. چون مساحت مستطیل برابر bh است .پس مساحت مثلث اولیه، نصف این مساحت خواهد بود.
محاسبه مساحت مثلث
روش هندسی
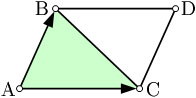 |
| محاسبه مساحت متوازی الاضلاع با استفاده از ضرب خارجی دو بردار |
مساحت یک متوازی الاضلاع را میتوان با استفاده از بردارها محاسبه کرد.اگر AB,AC را مطابق شکل فرض کنیم آنگاه مساحت ABCD برابر |AB × AC| خواهد بود.این مفدار ،اندازه ضرب خارجی دو بردار AB و AC میباشد.پس مساحت مثلث ABC برابر با نصف اندازه ضرب خارجی دو بردار AB و AC خواهد شد.
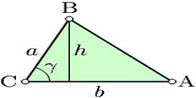 |
| استفاده از مثلثات برای پیدا کردن ارتفاع مثلث |
ارتفاع یک مثلث را میتوان با استفاده از روابط مثلثاتی بدست آورد.به عنوان مثال در شکل روبرو ارتفاع مثلث از فرمول
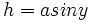 محاسبه میشود.اگر این فرمول را درفرمول
محاسبه میشود.اگر این فرمول را درفرمول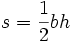 جایگذاری کنیم فرمول
جایگذاری کنیم فرمول 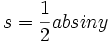 بدست می آید:
بدست می آید: فرض میکنیم نقطه A به مختصات (0, 0)یک راس از مثلث باشد و نقاط B به مختصات(x1, y1) و C به مختصات(x2, y2) دو راس دیگر مثلث باشند.در این صورت مساحت مثلث نصف مقدار|x1y2 − x2y1| خواهد شد.
راه دیگر محاسبه مساحت مثلث استفاده از فرمول heron است. این فرمول به صورت زیر است:
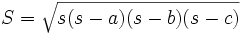 |
روش برداری
روش مثلثاتی
روش مختصاتی
فرمول heron