تابع ‎ $F(x)$ ‎ یک پاد مشتق ‎ $f(x)$ ‎ بر بازه $I$ است، هرگاه دو تابع فوق بر روی $I$ تعریف شده باشند و مشتق ‎ $F(x)$ ‎ ،‎ $f(x)$ ‎ باشد. یعنی به ازای هر عضو بازه $I$ داشته باشیم:

$\frac {dF(x)}{dx}=F$

[ شنبه 92/2/7 ] [ 6:29 صبح ] [ محمد رضا جبین پور ] [ نظرات () ]

پاد مشتق

پاد مشتق

$\frac {dF(x)}{dx}=F$

[ شنبه 92/2/7 ] [ 6:26 صبح ] [ محمد رضا جبین پور ] [ نظرات () ]

انتگرال

انتگرال

اَنتِگرال (integral) مقدار مشترک ممکن زیرین? مجموعه‌ای ریمانی و زبرین? مجموعه‌ای ریمانی یک تابع حقیقی در باز? مفروض است.^[1] انتگرال از مفاهیم اساسی در ریاضیات است که در کنار مشتق دو عملگر اصلی حساب دیفرانسیل و انتگرال را تشکیل می‌دهند.

نخستین بار لایب نیتس نماد استانداردی برای انتگرال معرفی کرد.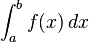

$\int_{a}^{b} f(x)\, dx$

aو b نقاط ابتدا و انتهای بازه هستند و $f(x)$ تابعی انتگرال‌پذیر است و $dx$ نمادی برای متغیر انتگرال‌گیری است.

از لحاظ تاریخی $dx$ یک کمیت بی نهایت کوچک را نشان می‌دهد. هر چند در تئوری‌های جدید، انتگرال‌گیری بر پایه متفاوتی پایه گذاری شده است.

محتویات

انتگرال نامعین

تعریف:

هرگاه معادله دیفرانسیلی تابعی معلوم باشد و بخواهیم معادله اصلی تابع را معلوم کنیم این عمل را انتگرال نامعین نامیده و آن را با نماد $\int$ نمایش می‌دهند. به انتگرال نامعین ضد مشتق نیز گفته می‌شود, زیرا عمل انتگرال نامعین گرفتن دقیقا برعکس عملیات مشتق‌گیری است.

بنا به تعریف نماد $\int{f(x)}.dx$ را انتگرال نامعین نامیده وحاصل آن را تابعی مانند $F(x)+c$ در نظر می‌گیریم هرگاه داشته باشیم:

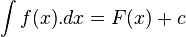
$\int{f(x)}.dx=F(x)+c$

در واقع می‌توان چنین بیان کرد:

$F$

مثال: مقدار انتگرال تابع $f(x)=\sqrt{x} + 2x^2 - 8$ را حساب کنید:

$\int{f(x)}.dx=\int{( x^{ \frac{1}{2}}+2x^2-8)}.dx = \int{ x^{\frac{1}{2}}}.dx + 2 \int{x^2}.dx - 8 \int{dx} = \frac{2}{3}x^{\frac{3}{2}}+ \frac{2}{3}x^3-8x+C$

$\Rightarrow \int{f(x)}.dx=\frac{2}{3}x\sqrt{x}+ \frac{2}{3}x^3-8x+C$

انتگرال معین

بنا به تعریف، نماد $\int_a^b f(x).dx$ را انتگرال معین نامیده و حاصل آن را به ازای $a<x<b$ عددی به صورت زیر تعریف می‌کنیم:

$\int_a^b f(x).dx=F(x)|_a^b=F(b)-F(a)$

$a$ و $b$ به ترتیب، کرانهای بالا و پایین انتگرال نامیده می‌شوند.

تابع انتگرال‌پذیر

اگر تابعی دارای انتگرال باشد به آن انتگرال‌پذیر گویند.

تعبیر هندسی انتگرال

از نظر هندسی انتگرال برابر است با مساحت سطح محصور زیر نمودار.

نکته انتگرال نمودار سه بعدی(انتگرال دو گانه)معرف حجم محصور زیر نمودار است و انتگرال سه‌گانه معرف پارالل زیر نمودار است(غیرقابل تصور).

مثال

انتگرال یک تابع مثبت پیوسته در بازه (0,10) در واقع پیدا کردن مساحت محصور بین خطوط x=0 , x=10 و خم منحنی $f_x$ است. aو b نقاط ابتدا و انتهای بازه هستند و f تابعی انتگرال‌پذیر است و dx نمادی برای متغیر انتگرال گیری است.

نمایش گرافیکی انتگرال.

انتگرال یک تابع مساحت زیر نمودار آن تابع است.

انتگرال گیری

(محاسبه انتگرال) انتگرال گیری به معنی محاسبه سطح زیر نمودار با استفاده از روشها وقوانین انتگرال گیری است.

مهم‌ترین تعاریف در انتگرال

از مهم‌ترین تعاریف در انتگرال می‌توان از انتگرال ریمان و انتگرال لبگ است. انتگرال ریمان به‌وسیله برنهارد ریمان در سال 1854 ارائه شد که تعریف دقیقی را از انتگرال ارائه می‌داد تعریف دیگر را هنری لبگ ارائه داد که طبق این تعریف شرایط تعویض پذیری حد و انتگرال با شرط مساوی ماندن عبارت، ارائه می‌کرد. از دیگر تعاریف ارائه شده در زمینه انتگرال می‌توان به انتگرال ریمان–استیلتیس اشاره کرد. پس به طور خلاصه سه تعریف زیر از مهم‌ترین تعاریف انتگرال می‌باشند:

محاسبه انتگرال

اکثر روش‌های اساسی حل انتگرال بر پایه قضیه اساسی حساب دیفرانسیل و انتگرال بنا نهاده شده است که بر طبق آن داریم:

1.f تابعی در بازه (a,b) در نظر می‌گیریم. 2.پاد مشتق f را پیدا می‌کنیم که تابعی است مانند f که و داریم: 3.قضیه اساسی حساب دیفرانسیل و انتگرال را در نظر می‌گیریم:

بنابراین مقدار انتگرال ما برابر خواهد بود.

به این نکته توجه کنید که انتگرال واقعاً پاد مشتق نیست (یک عدد است) اما قضیه اساسی به ما اجازه می‌دهد تا از پاد مشتق برای محاسبه مقدار انتگرال استفاده کنیم. معمولاً پیدا کردن پاد مشتق تابع f کار ساده‌ای نیست و نیاز به استفاده از تکنیکهای انتگرالگیری دارد این تکنیکها عبارت‌اند از :

انتگرال گیری به‌وسیله تغییر متغیر
انتگرال گیری جزء به جزء : $\int u\, dv=uv - \int v\, du$
انتگرال گیری با تغییر متغیر مثلثاتی
انتگرال گیری به‌وسیله تجزیه کسرها

روش هایی دیگر نیز وجود دارد که برای محاسبه انتگرالهای معین به کار می‌رود همچنین می‌توان بعضی از انتگرال‌ها با ترفند هایی حل کرد برای مثال می‌توانید به انتگرال گاوسی مراجعه کنید.

تقریب انتگرالهای معین

محاسبه سطح زیر نمودار به‌وسیله مستطیل هایی زیر نمودار. هر چه قدرعرض مستطیل‌ها کوچک می‌شوندمقدار دقیق تری از مقدار انتگرال بدست میآید.

انتگرال هایی معین ممکن است با استفاده از روش‌های انتگرال گیری عددی، تخمین زده شوند.یکی از عمومی‌ترین روش‌ها، روش مستطیلی نامیده می‌شود در این روش ناحیه زیر نمودار تابع به یک سری مستطیل تبدیل شده و جمع مساحت آنها نشان دهنده مقدار تقریبی انتگرال است. از دیگر روش هایی معروف برای تخمین مقدار انتگرال روش سیمپسون و روش ذوزنقه‌ای است. اگر چه روش‌های عددی مقدار دقیق انتگرال را به ما نمی‌دهند ولی در بعضی از مواقع که انتگرال تابعی قابل حل نیست یا حل آن مشکل است کمک زیادی به ما می‌کند.

کاربرد

انتگرال‌ها در واقع مساحت محصور در زیر نمودار هستند و در فیزیک می‌توان برای کاربردهای زیادی تعریف کرد مانند کار انجام شده در یک فر آیند ترمودینامیکی از انتگرال رابطه فشار و حجم به دست می‌آید. اما به طور کلی می‌توان آن را تغییرات کمیت حاصل ضرب افقی و عممودی نمودار نامیدمثلا: در یک رابطه کمیت‌ها را تحلیل ابعادی می کنیم مثلا رابطه سرعت و زمان را به صورت زیر نوشته می‌شود:

$v=[L]/[T] t=[T] \!$

سپس دو تحلیل را در هم ضرب می کنیم:

$[L] \!$

پس مساحت محصور در زیر نمودار برابر با تغییرات طول (جابجایی) است.

[ جمعه 92/2/6 ] [ 6:41 صبح ] [ محمد رضا جبین پور ] [ نظرات () ]

ادبیات ریاضیات

یاد ایامی که سهمی از ریاضی داشتیم

مغز خود رابا قوانین حساب انباشتیم

یاد ایامی که با یک عالم از سر زندگی

پای خود را در مسیر هندسه بگذاشتیم

یاد ایامی که مشتق در صدامان زنده بود

دست انتگرال؛ مارا از تنفس کنده بود

جذر ما مجذور دنیا بود و بی اندازه تا

بی نهایت در صداهامان صدا افکنده بود

یاد ایامی که دستان ریاضی مثل باد

دست ما را در سکوت زندگی مان می فشرد

یاد آن ایام شیرین ای دریغا ای دریغ

غنچه ما از خستگی نشکفته بود

[ پنج شنبه 92/2/5 ] [ 6:17 صبح ] [ محمد رضا جبین پور ] [ نظرات () ]

مادر حضرت عباس (ع) که بود؟

مادر حضرت عباس (ع) که بود

حضرت ام البنین یکی از از مادران نمونه تاریخ قلمداد می شود و تا هستی بر جاست و صفات حضرت عباس(ع) بر زبان ها جاری است سخن از مادرش ام البنین هم می شود، چرا که درس ادب، ولایتمداری، عشق به همنوع و آشنایی با دردهای زمان از جمله درس هایی بود که چهار پسر ام البنین در مکتب مادر آموختند و با آنها جاودانه شدند.

خورشید همواره در چشمان مادرانی طلوع می کند که به دوردست ها خیره شده اند و برای فرداها مردان و زنانی می پرورانند تا در زمین، این امانت الهی جانشین آسمانی باشند. دامان تربیت مادران مهد پرورش انسان های پاک و خدایی است. یکی از مادران برجسته تاریخ "ام البنین، فاطمه کلابیه" است که زندگی او مالامال از عشق به ولایت و امامت بوده و در تربیت فرزندان دلیر و شجاع و با ادب چون عباس بن علی (ع) بسیار موفق بوده است. تولد و رشد او در خاندان با اصالت و شجاع، صفات و ویژگی های فردی این بانو و صبر و بردباری در خانه امامت و تربیت فرزندانی که همگی پیرو امام خویش بوده و تا آخرین لحظات زندگی خویش دست از ولایت نکشیدند و پیام رسانی و مبارزه سیاسی این بانوی کریمه همه و همه نشان از مجد و عظمت وی دارد.

مادر بزرگوار حضرت ابوالفضل نامش فاطمه، کنیه اش ام البنین، نام پدر حزّام و برخی گفته اند حرام و برخی گفته اند خلّه، نام مادرش شهامه و برخی گفته اند لیلی. مورخان سال ولادت او را یادآوری نکرده اند لکن متذکر شده اند که تولد پسر ارشد وی عباس در سال 26 هجری بوده در نتیجه وقوع ولادت ام البنین را حدود 5 سال پس از هجرت تخمین می زنند.

ده سال پس از رحلت حضرت رسول(ص) و حضرت فاطمه(س) بنا بر وصیت خود حضرت فاطمه(س) حضرت علی (ع) درپی انتخاب همسر دیگری بود. برادرش عقیل را که در علم نسب شناسی وارد بود و قبایل و تیره های گوناگون و خصلت ها و خصوصیات اخلاقی و روحی آنان را خوب می شناخت طلبید از عقیل خواست که برایم همسری پیدا کن شایسته و از قبیله ای که اجدادش از شجاعان و دلیرمردان باشند..

عقیل یکی از کسانی بود که تفکر و گفته اش در علم انساب حجت بوده. عقیل بانو ام البنین از خاندان بنی کلاب را که در شجاعت بی مانند بود برای حضرت انتخاب کرد و حضرت علی(ع) این انتخاب را پسندید و عقیل را به خواستگاری نزد پدر ام البنین فرستاد. ام البنین دختری پاکدل و با تقوا بود. وی شرافت خانوادگی و اصالت ذاتی و پاکی فطری را یکجا به همراه داشت. زندگانی ام البنین همواره با بصیرت و نور دانش همراه بود و این ویژگی والا در جای جای کتب تاریخی ذکر شده است و ما را با عظمت این بانوی عالمه و فاضله آشنا می سازد.

حضرت ام البنین، امیرالمومنین(ع) را تنها همسر خود نمی دانست او را ولی و امام خود می دانست این نهایت بینش و بصیرت و علم و دانایی است که محور زندگی فردی امام و مولای او باشد. ام البنین (س) که از دامان خاندانی ادب پرور برخاسته بود در محضر اسوه ادب - علی(ع)- آن را بارور ساخت و الهی گردانید. او در پیشگاه خدا ادب بندگی نگاه می داشت و نسبت به مردم فروتن بود؛ ولی بزرگترین نمود ادب او در برابر علی(ع) و فاطمه(س) و فرزندان معصوم (ع) آنان است.

حضرت ام البنین خود را نه به عنوان جانشین فاطمه(س) بلکه به عنوان خادم فرزندان فاطمه(س) می دانست. عباس(ع) از این سرچشمه ادب، تربیت آموخت که برادرش حسین(ع) را همیشه یا سیدی، یا اباعبدالله خطاب می کرد. اگر چه هر دو از یک پدر بودند اما تواضع و ادب او نسبت به حسنین(ع) به علت نگرش عمیق او به عظمت حضرت زهرا(س) بوده و این درسی است که از کودکی حضرت ام البنین به آنها آموخت.

امر مقدس تربیت برای زنان به عنوان یک امتیاز مهم مطرح شده است که در این راستا ام البنین یکی از از مربیان تاریخ قلمداد می شود تا هستی بر جاست و صفات عباس(ع) بر زبان ها جاری است سخن از ام البنین می شود. آری درس ادب، ولایتمداری، عشق به همنوع و آشنایی با دردهای زمان از جمله درس هایی بود که چهار پسر ام البنین در مکتب مادر آموختند و با آنها جاودانه شدند. ام البنین پس از واقعه عاشورا وفات کرد و در بقیع و در نزدیکی فاطمه زهرا(س) به خاک سپرده شد.

ابونصر نجاری در کتاب خود به نام "سرالسلسله العلویه" می گوید: امیرمومنان پس از فاطمه(س) از قبیله فهد تنها از ام البنین فرزند داشت و او پیش از آن حضرت و نیز پس از وفات او با کس دیگر ازدواج نکرد.

عمر رضا کحّاله در "اعلام النساء" می گوید او شاعری خوش بیان بود. همچنین شاعر توانا، شیخ احمد دجیلی گفته است: ام البنین و ما اسمی هذایاک خطوت بالصبر و الایمان ذکراک / ای ام البنین! چقدر از خصوصیات والایی برخورداری به سبب شکیبایی و ایمانت، یاد تو جاودانه شد.

[ چهارشنبه 92/2/4 ] [ 10:0 صبح ] [ محمد رضا جبین پور ] [ نظرات () ]

خوارزمی

زندگی نامه خوارزمی

ابو عبدالله محمد بن موسی خوارزمی که ریاضیدانان اروپا او را algoritmus می خوانند یکی از نخستین و بزرگترین ریاضیدانان و اختر شناسان ایران است که در بغداد کار میکرد .از زندگی و خانواده او آگاهی زیادی در دست نیست جز در حدود سال 175 - 180 هجری - در خوارزم متولد و هنگام جوانی در خزانه الحکمه مامون مشغول به کار و تحقیقات شد و پس از سالها فعالیت شبانه روزی بلاخره در حدود سال 225 - 232 هجری - دعوت حق را لبیک گفته و به دیار باقی شتافت .

برخی ار تاریخ نویسان عنوان مجوسی را به دنبال نام او اورده اند ، معلوم میشود در خانواده ای با فرهنگ از زرتشتیان خوارزم زاده شد و به همین مناسبت به احتمال قوی به نوشته های علمی ایرانی پیش از یورش عرب دسترسی داشته است

زمان خوارزمی :

روزگار خوارزمی به روزگار زرین در دوران حکومت خلیفه های عربی معروف است . روزگاری که هارون بر سرزمین های خلافت شرقی فرمان میراند . این روزگار دوران شکفتن فرهنگی است که مرکز ثقل آن در ایران بوده است

زندگی خوارزی با خلافت مامون متقارن بود . مامون به کوشش و همراهی طاهر فرزند حسین معروف به ذوالیمینین بر برادر خود امین پیروز شد.

کارهای خوارزمی در زمینه اختر شناسی :

نخستین اثری که خوارزمی در بغداد نوشت ، تنظیم جدول سینوس ها بود . خوارزمی این اثر خود را با توجه به کارهای بطلمیوس و جدول های دانشمندان هندی تنظیم کرد . ولی خود آنها را مورد تحقیق قرار داد و در نتیجه جدول او به مراتب دقیق تر از جدول های یونانی و هندی است

در واقع سه اثر خوارزمی

زیج الاول
زیج الثانی
السند هند الصغیر

به رصد هایی که در زمان مامون صورت گرفت به سیدهانتا مربوط میشود .زیرا سند هند همان سیدهانتای هند است . سیدهانتا به چند کتاب اختر شناسی و ریاضی گفته می شود که در هند تنظیم شده است و کهن ترین آنها مربوط به نیمه نخست قرن پنجم میلادی است .یکی از این کتابها در زمان منصور خلیفه دوم عباسی به بغداد آورده شد و توسط ابراهیم فرزند حبیب فزاری به یاری مانکا ، صفیر هند در بغداد ترجمه شد و ریاضیدانان و اختر شناسان حوزه خلافت بغداد برای نخستین بار با دانش ریاضی و اختر شناسی هند آشنا شدند .

ترجمه فزاری تا زمان خوارزمی مبنای کار اخترشناسان بود ولی پس از آن که خوارزمی دو زیج خود را ارائه کرد مرجع مطمئن تری برای اختر شناسان پدید آمد . خوارزمی در تنظیم این دو زیج به احتمال قوی روش تلفیقی خود را با استناد به دانش های یونانی ، هندی و ایرانی به کار برده است

خوارزمی از راه ترجمه سیدهاتنا با مکتب ریاضی و اختر شناسی هند و از راه ترجمه مجسطی کتاب بطلمیوس با مکتب یونانی آشنا شد. خوارزمی ترجمه هایی از نوشته های ارسطو و اقلیدس و دیگران با مکتب یونانی آشنا شد .به جز آنکه به خاطر بستگی هایی که با پاسداران فرهنگ ایرانی داشت کم و بیش از دانش نیاکان خود با خبر بود . رساله های زیج اول و زیج دوم خوارزمی به احتمال زیاد بر اساس دو رصدی که اولی در بغداد و دومی در دمشق انجام گرفت نوشته شده است

نوشته های خوارزمی در زمینه اختر شناسی و جغرافیای ریاضی اثر زیادی در کارهای دانشمندان بعدی داشته است. در واقع مسلمه مجریطی صورت تازه ایی از جدول هاب فلکی را بر اساس کارهای خوارزمی تنظیم کرد و همین جدول های مجریطی است که اساس کار اخترشناسان اروپای غربی قرار گرفت

صورت الارض

نخستین اثر علمی در دوران تازه شکوفایی دانش در زمینه جغرافیا دانست . خوارزمی واژه صورت الارض را به همان معنایی به کار برده است که ما امروز آن را جغرافی می نامیم

گرچه این کتاب بر اساس جغرافیای بطلمیوس تنظیم شده است ولی به هیچ وجه نمیتوان آن را ترجمه ای از جغرافیای وی دانست خوارزمی در این کتاب تقسیم بندی مطالب را به صورتی غیر از جغرافیای بطلمیوس انجام داده است و تحت تاثیر فرهنگ و باورهای ایرانی به تقسیم بندی اقلیم های هفت گانه گرایش دارددر حالی که بطلمیوس از بیست و یک ناحیه نام میبرد با وجود این ها باید گفت که خوارزمی برای نوشت کتاب صورت الارض کتاب جغرافیای بطلمیوس را پیش روی خود داشته است

کارهای خوارزی در زمینه حساب و جبر :

کارهای خوارزی در زمینه حساب و جبر در تاریخ ریاضیات و از دیدگاه مسیر تکاملی ریاضیات اهمیت بسیار زیادی دارد

تالیف خوارزمی در باره حساب به نام

حساب الهند

این کتاب تنها از طریق ترجمه لاتینی آن به ما رسیده است و نسخه منحصر به فرد این ترجمه به زبان لاتینی و با عنوان Algorithmi numero indorum در کتابخانه دانشگاه کمبریج نگهداری میشود

این کتاب در پیشرفت بعدی ریاضیات در اروپای غربی و جنوبی نقشی اساسی داشته است زیرا اروپای غربی و جنوبی نقشی اساسی داشته است . زیرا اروپایی ها به وسیله آن با روش هندی عدد نویسی یعنی نمادهای ده گانه هندی با به کر بردن صفر و استفاده از نظام موضعی بودن رقم ها آشنا شدند

از آنجا که در اروپای غربی و جنوبی این شکل عدد نویسی را از کتابی یاد گرفتند که به زبان عربی نوشته شده بود و نویسنده آن نیز در کشور های عربی زبان زندگی میکرد رقم های هندی دستگاه عدد نویسی دهدهی را به اشتباه رقم های عربی نامیدند

خوارزمی مسئله هایی را که به معادله درجه اول منجر می شود از راه حسابی و با روش های یک فرضی و دو فرضی حل میکند روش یک فرضی همان روشی است که امروز هم با نام راه حل فرضی مورد استفاده قرار میگیرد و خوارزمی آن را از هندی ها گرفته است

روش دوم یعنی روش دو فرضی به این ترتیب بود که با فرض دو عدد دلخواه برای مجهول هر بار میزان اشتباه را به دست آورده و به کمک انها مقدار واقعی مجهول را محاسبه می کرد . اگر به زبان نمادهای امروزی جبر صحبت کنیم ، روش دو فرضی را میتوان به این ترتیب شرح داد

فرض کنید f(x) = p ، که در آن f(x)تابعی خطی نسبت به xو p مقدار تابت باشد در آغاز x=aو سپس x=bو به دست می اوریم

f(a) = Aو f(b) = B

P-A را با E و P-Bرا با K نشان می دهیم در این صورت داریم

X = (bE - Ak)/(E - K)

البته به گمان خوارزمی رابطه ای که در اینجا به دست می آید و به یاری آن میتوان مقدار مجهول را پیدا کرد تصادفی است

جبر

کتاب جبر خوارزمی نقشی بسیار اساسی در تاریخ ریاضیات داشته و نمونه مشخصی است از پژوهش های ریاضیدانان ایرانی در دوره ای از تکامل ریاضیات که سمتگیری کاربردی داشته است .این کتاب بعدها به زبان لاتین ترجمه شد و برای مدتی طولانی تنها کتاب درسی ریاضیات در اروپای غربی بود

برخی از مطالب این کتاب ، کارهای دیوفانت و دانشمندان هندی را به یاد می آورد و به همین مناسبت برخی گمان می بردند که خوارزمی از این سرچشمه ها استفاده می کرده است ، برخی از روش هایی که خوارزمی برای حل معادله به کار برده ما رو به یاد دیوفانت می اندازد ولی خوارزمی به هیچ وجه از کوتاه نویسی که خاص جبر دیوفانت است استفاده نمی کند و اصطلاح های او را به کار نمی برد به جز این بررسی های تاریخی نشان داده است که آشنایی دانشمندان دربار خلیفه عربی با کارهای دیوفانت بعد از تنظیم کتاب خوارزمی بوده است

به همین ترتیب به دلیل اختلاف هایی که بین روش های خوارزمی با روش های دانشمندان هندی در حل معادله ها وجود دارد میتوان نتیجه گرفت که او در کتاب جبر و مقابله خود از روش های هندی هم پیروی نکرده است

جبر خوارزمی حتی از دیدگاهی که دنبال می کند ارتباطی با جبر یونانی ندارد یونانی ها در بخش عمده ای از کارهای خود هیچ ضرورتی نمیدیدند که به کاربرد مفهوم های عملی توجه کنند در حالی که خوارزمیدرست برعکس عمل میکرد و تلاش او در اینت جهت بود که علم را به خدمت زندگی بگمارد هدف علمی آن را بشناسد و بشناساند . جبر خوارزمی بخش های ویژه ای درباره تجارت ، تقسیم ارث و عمل کردن به وصیت ها دارد و بر خلاف یونانی ها که همه چیز را به هندسه منجر می کردند خوارزمی برخی از مسئله های هندسی را با یاری معادله حل میکند

ارزش علمی کار خوارزمی در این است که کتاب او تنها رساله ای درباره حل مسئله نیست بلکه خوارزمی الگوریتم حا معادله ها را مطرح میکند کاربرد آن را هم توضیح میدهد و هر جا لازم می بیند از روش های هندسی هم سود می جوید

واژه جبر که خوارزمی برای نامیدن این شاخه از دانش ریاضی انتخاب کرده است معرف درستی این اندیشه است . خوارزمی جبر را به معنای جبران کردن می گرفت که به زبان امروزی به معنای انتقال یک عدد با یک جمله منفی از یک سمت به سمت دیگر معادله است که آن را به عدد یا جمله ای با ضریب مثبت تبدیل می کند

در کنار واژه جبر به واژه مقابله بر میخوریم که معرف عمل دیگری در معادله است : معادل قرار دادن دو عبارت برابر در دو سمت معادله

بهاء الدین عاملی معروف به شیخ بهائی ریاضیدان آغاز سده شانزدهم میلادی خیلی خوب دو واژه جبر و مقابله را تعریف میکند ، شیخ بهائی می گوید :

قسمتی از معادله را که شامل مقدار منفی است ممیتوان حذف کرد و به طرف دیگر معادله افزود این عمل را جبر گویند جمله های مشابه را میتوان از دو طرف معادله حذف کرد این عمل مقابله است

عمل های جبر و مقابله به زبان امروزی ، عبارتند از انتقال جمله ای از یک سمت به سمت دیگر معادله - با تغیر علامت - و جمع جبری جمله های مشابه

در کتاب جبر خوارزمی راه حل معادله های درجه اول و دوم شرح داده شده است درست است که خوارزمی برای حل معادله های درجه دوم به ظاهر راه حل کلی نمیدهد و با تقسیم معادله های درجه دوم به پنج گونه مختلف برای هر کدام راه حلی جداگانه ارائه می کند ولی ضمن حل نمونه های عددی اغلب همان دستوری را دنبال میکند که امروز برای حا معادله های درجه دوم می شناسیم - نمونه معادله حل شده توسط خوارزمی و مقایسه با روش امروزی در صفحه 74 الی 79 کتاب نگاهی به تاریخ ریاضیات در ایران اثر پرویز شهریاری -

نام خوارزمی در آغاز با ترجمه کتاب حساب الهند او به اروپا رفت و الخوارزمی به صورت لاتینی شده آن الگوریتموس تبدیل شد و بعد ها به تدریج در تمامی اروپای غربی و جنوبی با نام الگوریتموس و بعد ها الگوریتم از راه عدد نویسی هندی آشنا شدند . ولی به تدریج این اصطلاح به هر دستگاه یا دنباله ای از محاسبه داده شد

به این نکته باید توجه کرد که واژه الگاریتم هیچ ربطی با واژه الگوریتم ندارد در ضمن الگوریتموس در آغاز در اروپای غربی به معنای محاسبه شمرده می شد و بعد ها به شاخه ای از منطق ریاضی شمرده شد

نامی که خوارزمی بر کتاب جبر خود گذاشته است امروز در همه زبان های زنده دنیا باقی مانده است : در زبان فرانسوی Algebre ، در زبان انگلیسی Algebra، در زبان روسی آلگبر و غیره . میبینیم حتی حرف تعریف ال هم از ابتدای آن حذف نشده است

تا بیش از نیم سده پیش در ایران کتاب های درسی و غیر درسی جبر را با عنوان جبر و مقابله می نوشتند

یکی از کارهای پر ارزش خوارزمی قبل ار پیدایش نمادها و واژه های تازه پیدا کردن واژه و اصطلاح های مناسب در قلمرو جبر بود برای نمونه برای مجهول از واژه شیء استفاده می کرد و آن را درست به همان مفهومی که امروز از نماد Xاستفاده می کنیم به کار می برد . انتقال این واژه به اروپا و نوشتن آن به صورت X در آغاز نماد x و سپس سایر نماد ها را برای بیان مقدارهای مجهول به وجود آورد

از میان کتاب های خوارزمی تنها کتاب جبر او به همت زنده یاد حسین خدیو جم به فارسی بر گردانده شده است

کتاب جبر و مقابله خوارزمی دو بخش دارد که در بخش اول به حل مسئله هایی درباره شش نوع معادله صحبت میکند و راه حل ها همه جبری و گاه هندسی اند و در بخش دوم از کاربرد ها بحث میکند و نمونه هایی از مسئله هایی می آورد که بیشتر مربوط به تقسیم ارث و عمل به وصیت هاست

کتاب خوارزمی ابتدا در اروپا در قرن ششم - سده دوازدهم میلادی - توسط جراد کرمونایی ترجمه شد در همین سده ترجمه دیگری از رابرت چستری باز هم به زبان لاتین انجام گرفت و از قرن هشتم - قرن شانزدهم میلادی - ابتدا توسط آدریان رومانوس و سپس دیگران کتاب را به زبان های مختلف اروپایی ترجمه کردند

[ سه شنبه 92/2/3 ] [ 6:18 صبح ] [ محمد رضا جبین پور ] [ نظرات () ]

میزان اضطراب ریاضی دختران و پسران!!!

تحقیقات جدیدی که در دو دانشگاه آکسفورد و کمبریج انجام گرفته نشان می‌دهد دختران بیشتر از پسران تحت تاثیر اضطراب ریاضی قرار می‌گیرند.
محققان در این مطالعه نشان دادند دخترها بیشتر از پسرها تحت تاثیر اضطراب ریاضیقرار گرفته و همین آنها را در موفقیت در امتحان‌های ریاضی عقب‌تر از پسرها نگه می‌دارد.

گفته می‌شود که ریاضی همواره به عنوان موضوعی مردانه نمایش داده شده و این به آن معنی است که بسیاری از زن‌ها خود را افرادی تصور کنند که دچار ضعف ریاضی هستند. دانشمندان دانشگاه‌های آکسفورد و کمبریج اعلام کردند عملکرد دختر‌ها و پسرها به صورت مستقل در امتحانی یکسان برابر بوده است.

محققان همچنین اعلام کردند دختر‌ها بدون حضور احساساتی از قبیل دلهره،‌ بی‌علاقگی،‌ اضطراب،‌ نگرانی،‌خستگی و ترس در مقابله با مسایل ریاضی از پسرها پیشی خواهند گرفت. همچنین در این مطالعه اعلام شده است که بالا بودن میزان اضطراب ریاضی در بریتانیا حاصل پایین بودن تعداد دانش‌اموزانی است که تحصیل در رشته ریاضی را برای آینده خود انتخاب می‌کنند.

به گفته دنس ژوکس از دپارتمان روانشناسی تجربی دانشگاه کمبریج،‌ اضطراب ریاضی عاملی است که توضیح می‌دهد چرا تنها هفت درصد از کودکان در سطح بالا به مطالعه ریاضی می‌پردازند و تعداد آنهایی که در دانشگاه‌ها این رشته را انتخاب می‌کنند رو به کاهش است.

در این مطالعه روی 433 دانش‌آموز دبیرستانی در بریتانیا تحقیق شده‌است. این داوطلبان 11 تا 15 ساله در امتحان‌های ریاضی حضور یافته و از آنها خواسته شد پاسخنامه امتحان را تکمیل کنند و به صورت همزمان واکنش‌های فیزیولوژیکی،‌ احساسی،‌ شناختی و رفتاری آنها مورد ارزیابی قرار گرفت.

نتایج این آزمون‌ها هیچ تفاوتی در توانایی حل مسایل ریاضی بین دختر‌ها و پسر‌ها نشان نداد اما نشان داد که میزان اضطراب ریاضی دختر‌ها بالاتر از پسر‌هاست و درصورتی که این اضطراب حذف شود،‌ دخترها عملکرد بالاتری از پسرها در حل مسایل ریاضی از خود نشان می‌دهند.

[ یکشنبه 92/2/1 ] [ 6:49 صبح ] [ محمد رضا جبین پور ] [ نظرات () ]

نمونه سوال ریاضیات دوم راهنمایی

آزمون های پایانی سال دوم-خرداد 91

استان آذربایجان شرقی - خرداد 91	استان فارس - خرداد 91
استان آذربایجان غربی - خرداد 91	استان قزوین - خرداد 91
استان اردبیل - خرداد 91	استان قم - خرداد 91
استان اصفهان - خرداد 91	استان کردستان - خرداد 91
استان البرز - خرداد 91	استان کرمان - خرداد 91
استان ایلام - خرداد 91	استان کرمانشاه - خرداد 91
استان بوشهر - خرداد 91	استان کهگیلویه و بویراحمد - خرداد 91
استان تهران - خرداد 91	استان گلستان - خرداد 91
استان چهارمحال و بختیاری - خرداد 91	استان گیلان - خرداد 91
استان خراسان جنوبی - خرداد 91	استان لرستان - خرداد 91
استان خراسان رضوی - خرداد 91	استان مازندران - خرداد 91
استان خراسان شمالی - خرداد 91	استان مرکزی - خرداد 91
استان خوزستان - خرداد 91	استان هرمزگان - خرداد 91
استان زنجان - خرداد 91	استان همدان - خرداد 91
استان سمنان - خرداد 91	استان یزد - خرداد 91
استان سیستان و بلوچستان - خرداد 91	آزمون هماهنگ خارج از کشور - خرداد 91

[ شنبه 92/1/31 ] [ 6:30 صبح ] [ محمد رضا جبین پور ] [ نظرات () ]

افلاطون

افلاطون در سال 427 قبل از در خانواده ای اشرافی به دنیا آمد. در 18 سالگی با سقراط آشنا شد و مدت 10 سال را به شاگردی سقراط به سر برد. بعد از اعدام سقراط یک سلسله سفر را آغاز کرد که در طی این سفرها از نقاط مختلفی از جهان نظیر مصر و سیسیل و فلسطین دیدن کرد که در این سفرها با اندیشه های متفاوتی آشنا شد که تاثیر آنها در افکار افلاطون هویدا است.هنگامی که افلاطون به آتن بازگشت 40 سال داشت. در این زمان بود که مدرسه معروفش را به نام آکادمی تاسیس کرد. این مدرسه را می توان اولین دانشگاه محسوب کرد که در آن دروسی نظیر فلسفه ریاضیات و نجوم تدریس می شد. برای مطالعه افلاطون یقینا بهترین منبع همان آثار اوست که در قالبی ادبی نوشته شده اند. با مطالعه این آثار به راحتی می توان به قریحه ادبی افلاطون پی برد. مهمترین و در عین حال کاملترین اثر افلاطون کتاب جمهوریت است. که او در این کتاب در باره مسایل فلسفی مختلفی سخن رانده است از اخلاق گرفته تا ساسیت و هنرو تربیت و مابعد الطبیعه سخن رانده است. با مطالعه نوشته های افلاطون می توان به سیر افکار او پی برد. کتب وی را می توانیم بر اساس دوره ای از زندگی که افلاطون اقدام به نگارش آن کرده است به سه دسته تقسیم بندی نماییم. دسته اول کتب و رسالاتی هستند که در دوران جوانی او نگاشته شده اند. نوشته های این دوران اکثرا دیالوگهایی بدون نتیجه گیری هستند. سمت و سوی نوشته های این دوران مربوط به فعالیت های تربیتی است. آثار دوره میانسالی بر خلاف دوره جوانی حاوی دیالوگهایی با نتیجه گیری است. درآثار این دوره است که مسایل اساسی فلسفه فلاطون نظیر ایده و مثل مطرح می گردد . اثر برجسته افلاطون در این دوره جمهوریت است. و بالاخره آثار دوران کهولت افلاطون که می توان آنها را آثار دوران پختگی و اصلاح آثار قبلی دانست .برای مثال از آثار این دوره می توان به قانون و نوامیس اشاره کرد. افلاطون در فلسفه راه استادش سقراط را دنبال کرد. بدین معنا که دغدغه اصلی او انسان بود و از فلاسفه طبیعی دور شد.اوقسمت زیادی از تلاش خود را معطوف به حل مسایلی نظیر اخلاق حق و عدالت کرد. او در جمهوریت مباحثه سقراط و شخص جدلی را به تصویر می کشد که سقراط و آن شخص در باره و معنا و مفهوم عدالت بحث می کنند. سقراط آن شخص به تعریف کردن مفهوم عدالت وامی دارد . که در نهایت آن شخص مجبور می شود که بگوید: حق در قدرت است و عدالت در نفع قویتر(نظیر بعضی از تعابیر نیچه). سپس وی از سقراط می خواهد که او نیز تعریفش را ارایه دهد که سقراط به نوعی از ارایه دادن تعریف طفره می رود و چنین پاسخ می دهد که عدالت نوعی رابطه سالم بین افراد در اجتماع است. بنابراین مطالعه آن به عنوان بخشی از جامعه و اجتماع راحت تر است. همانند اینکه بوسیله توصیف یک جامعه سالم توصیف یک فرد سالم راحتر می شود. افلاطون به این شکل حل مسئله اخلاق و عدالت را به اجتماع و به تبع آن مسایل سیاسی آن اجتماع مربوط می کند. در اینجاست که کم کم با فلسفه سیاسی افلاطون که از نکات برجسته هنگام مطالعه افلاطون است مواجه می شویم. او پس طرح مسایلی مانند اینکه حرص و طمع و یا برتری جویی سبب می شود که افراد و جوامع انسانی مدام با هم در کشمکش باشند . به این نتیجه می رسد که ابتدا باید انسان را از لحاظ روانشناختی مورد بررسی قرار دهد تا بوسیله آن به پی ریزی جامعه ای ایده آل نایل گردد. در روانشناسی افلاطون رفتار های انسان از سه منبع میل و اراده و عقل سرچشمه می گیرد .میل انسان شامل مواردی نظیر تملک شهوت غرایز می شود. مرکز امیال نیز در بدن شکم است.هیجان هم مواردی مانند شجاعت قدرت طلبی و جاه طلبی را در برمیگیرد. عقل نیز مسئول مواردی نظیر اندیشه و دانش و هوش است. منابع ذکر شده هم در افراد مختلف دارای درجات متفاوتی است. مثلا در بازاریان و کسبه عموم مردم میل است که نقش اصلی را در زندگی بازی می کند و در جنگجویان و لشگریان هیجان نقش اصلی را بر عهده دارد. و عقل نیز پایه رفتار حکما ست. بعد از این مقدمات افلاطون شروع به ترسیم جامعه آرمانیش می کند و برای ایجاد آن راهکاری هم ارایه می دهد. آرمانشهر او جامعه ایست که درآن هر کس با توجه به ذاتش یعنی همان منابع رفتاری که در فوق ذکر شدند در جای خودش قرار گرفته باشد مثلا کسی که میل در او بالا باشد فقط مشغول کسب و کار خود شود و در کار سیاست دخالت نکند یا کسی شجاعت و هیجان او در درجه ای بالا قرار داشته باشد شغلش در جامعه نظامی باشد. در آرمانشهر افلاطون سزاوارترین گروه برای حکومت فلاسفه هستند که در آنها عنصر عقل در درجه بالایی قرار دارد(نوعی از نخبه گرایی). اینجاست که افلاطون نیز مانند سقراط تمایلش را به آریستوکراسی (حکومت اشراف)نشان داده و به عناد با دموکراسی بر می خیزد.البته باید توجه داشت که اشراف یا شریفترین مردم برای حکومت الزاما کسانی نیستند که دارای قدرت و ثروت اند. بلکه باید این افراد دارای حکمت باشند تا شایستگی لازم را برای حکومت داسته باشند. و اما راهکار افلاطون برای تشکیل آرمانشهرش: ابتدا باید کودکان زیر 10 سال را جمع کرد و آموزش همگانی آنها را شروع کرد این آموزشها شامل مواردی مانند موسیقی ورزش و تعالیم مذهبی می شود.در این میان تعالیم مذهبی بر مبنای دین تک خدایی از اهمییت خاصی بر خوردارد است .افلاطون می خواهد از مذهب به عنوان عاملی برای کنترل توده های مردم استفاده کند به عقیده او اعتقاد به یک خدای قادر و مهربان و در عین حال قهار باعث می شود که کنترل رفتارهای مردم راحت تر شود و گرایش آنها به طرف جرم و جنایت خود به خود کم شود. این آموزشها تا سن 20 سالگی ادامه خواهند یافت. سپس در این سن از کلیه آموزش دیدگان امتحانی گرفته خواهد شد به شکلی که در این امتحان اکثریت شرکت کنندگان حذف شوند. این اکثریت به کسب و کار و بازار و کشاورزی و... مشغول خواهند شد. تربیت قبول شدگان این امتحان تا سن 30 که زمان بر گزاری امتحانی دوباره است ادامه خواهد داشت . مردود شدگان این دوره به مشاغلی نظیر سپاهیان و لشگریان را اشغال خواهند نمود . کسانی که این امتحان را نیز با موفقیت پشت سر بگذرانند آموزش آنها 5 سال دیگر هم طول خواهد کشید که در این 5 سال با مسایلی نظیر ریاضیات و فلسفه و ایده و مُثل افلاطونی سر خواهند کرد. با ایده و مُثل افلاطونی به زودی آشنا خواهیم شد. بعد از این 5 سال افراد آموزش دیده باید 15 سال را بین بقیه مردم بدون هیچ پشتوانه ای و به تنهایی زندگی کنند. که این نیز برای آنها نوعی امتحان محسوب می شود. بعد از از این 15 سال کسانی که این امتحان هم را با موفقیت یگذارنند آماده حکومت هستند.برای اینکه این افراد دچار فساد نشوند باید زندگی در سطح پایین و مانند سربازان داشته باشند. آنها از داشتن زن و فرزند اختصاصی محروم می شوند و زن و فرزند آنها اشتراکی خواهد بود تا مبادا به عشق به همسر و فرزند مانع وظیفه خطیر آنها گردد. بدین شکل حکومت تشکیل می شود که حاکمان آن بدون هیچ گونه رای گیری به قدرت میرسند و در عین حال مناسب ترین افراد هم برای حکومت هستند. در این شیوه هیچ چگونه نزاع و درگیریی هم برای تصاحب حکومت اتفاق نخواهد افتاد. از نظر افلاطون در چنین سیستمی است که حق و عدالت تحقق می یابند. زیرا هر کس بر حسب استعدادها و تواناییهایش در موقعیت مناسب خود قرار گرفته است و فرصت های محیطی بر ای افراد از طبقات مختلف یکسان است در حالی که در دیگر اندیشه های حتی اندیشه های پیشرفته امروزی نظیر لیبرال دموکراسی نیز چنین امکانی وجود ندارد. از این جهت افلاطون به کلی با دموکراسی یونان مخالف است. افلاطون جامعه را به شکل پیکره ای انسانی در نظر می گیرد. که حکام فیلسوف سر آن هستند . و سینه آن را سربازان و لشگریان تشیکل می دهد.مردم عادی نظیر بازرگانان پیشه وران و کشاورزان هم شکم آن هستند. به نوعی می توان گفت که افلاطون در اواخر عمر متقاعد شده بود که تشکیل دولت آرمانیش ممکن نیست. از این رو در کتاب قانون به تشریح دولتهای ناکامل می پردازد.معیار او برای طبقه بندی دول ناکامل نزدیکی آن دول به حکومت آرمانی اوست. او حکومت های ناکامل را بر اساس نزدیکی به آرمانشهرش به این دسته ها تقسیم بندی می کند: 1 تیموکراسی 2 الیگارشی 3 دموکراسی 4 جباری یا مستبد . حکومت تیومکراسی حکومت متفاخران است حکومتی مانند اسپارت . این نوع حکومت معمولا در اثر زراندوزی طبقه حاکم تبدیل به حکومت الیگارشی می شود که حکومت توانگران و ثروتمندان است. در این حکومت پول معیار همه چیز است. سرانجام این نوع حکومت هم افزایش زراندوزی در جامعه و به تبع آن ایجاد جامعه ای دو قطبی و ایجاد شکاف های عظیم اجتماعی است .که سر انجام آن انقلابی است که به دموکراسی می انجامد. دمکراسی هم حکومتی است که در آن افراد غیر متخصص بسیاری به امر حکومت مشغول اند. علاوه بر آن گروههای مختلف اجتماعی در آن دایما بر سر تصاحب حکومت در رقابت و نزاع به سر می برند. پس از آنکه یکی از این گروهها موفق به تصاحب کامل قدرت شد خود به خود حکومت دموکراسی از بین رفته است و حکومتی مستبد و یا به عبارتی دیگر جبارانه جایگزین آن گشته است. به نظر نگارنده این مطلب مهم ترین انتقادی که می توان به این جامعه آرمانی افلاطون وارد کرد این است که او تابلویی بی حرکت و منظم وماشین وار از جامعه ترسیم می نماید وتوجه کافی را به تغییر و تحول اجتماع و به خصوص افرادش را نمی کند. شاید بتوان گفت که در آرامان شهر افلاطونی فردیت افراد جامعه فدای تشکیل جامعه ای آرمانی می گردد. شاید این دید افلاطون به جامعه از همان نظریه "مثل" که پایه ای فلسفی او را تشکیل می دهد ناشی شده باشد.می توان نظریه مثل افلاطون را به طور خلاصه بدین شکل شرح داد: افلاطون نیز همانند هراکلیتوس و پارمنیدس همه دنیای اطرافمان را که به وسیله حواس از آن مطلع می شویم را دنیایی متحرک تغییرپذیر و فناپذیر می داند لذا او معتقد است دنیایی که ما بوسیله حواسمان درک می کنیم موضوع علم نیست و اصلا این دنیا کاملا واقعی نیست. دنیایی که ما حس می کنیم دنیایی است محدود به زمان و مکان و در قید تحرک و تغییر پذیری پس حقایق واقعی واصیل نمی تواند شامل این دنیای محسوس ما باشد. ودر سطح بالاتری از آن قرار دارد. محسوساتی که ما ادراک می کنیم ظواهر و پرتوهایی از آن حقایق اصیل هستند. افلاطون به هر یک از این حقایق که در عالم بالاتری قرار دارند مثال یا ایده می گوید. مثال برای افلاطون کاملا حقیقی ومطلق ولایتغیر است .این مثالها یا مثل فراتر از ابعاد مکان وزمان هستند لذا تنها راه شناخت وبررسی آنها به کار بردن عقل وخرد است. افلاطون به این شکل عالم را به دو قسمت عمده طبقه بندی می کند : قسمت اول دنیای محسوسات وظواهر که به وسیله حواس ادراک می شود و قسمت دوم عالم ایده ها و مثل که راه یافتن به آن بدون استفاده از عقل ممکن نیست. مثال معروفی که برای شرح مثل افلاطونی بیان می شود اسب مثالی است. ما ممکن است در طول زندگی خود اسبهای زیادی دیده باشیم. این اسبها از رنگها و نژادهای مختلفی بوده اند و احتمالا همه آنها با هم فرقهایی هر چند جزیی داشته اند. ولی ما در اینکه این موجودات اسب هستند و نه حیوانی دیگر مانند سگ شکی نداریم.دلیل این امر این است که در عالمی بالاتر مثال یا ایده ای حقیقی و کامل از اسب وجود دارد که اسبهایی که ما می بینیم از آن ایده اصیل سرچشمه و نشات گرفته اند. به بیان دیگر می توان اسب مثالی را به عنوان قالبی برای این اسبها محسوب کرد. این طبقه بندی افلاطون از عالم گاهی ریزتر نیز می شود مثلا دنیایی که انعکاسهاو سایه ها یا رویاها توهمات می سازند دنیایی است که از درجه حقیقی بود پایین تر از دنیا محسوسات قرار دارد و یا بین دنیای محسوسات و دنیای ایده ها که حقیقی ترین است دنیای علم ودانش و ادراکات ریاضی قرار دارد. البته افلاطون در دنیای مثلی هم سلسله مراتب قایل است به این شکل که ایده های کوچک ایده های بزرگتر را می سازند که در نهایت منجر به تشکیل حقیقتی واحد یا خدا می شوند. افلاطون به اثبات نظریه مثل خود نپرداخت و آن را در حد فرضیه باقی گزارد . به شکل که او وجود خدایش را هم قابل اثبات نمی داند و معتقد است که فقط با دیدن آثارش پی به وجود او می بریم ودر این زمینه بر اساس نظریه مثلش به همین مطلب اکتفا می کند که اگر گرایش به خیری ویا زیبایی وجود دارد پس خیر مطلق و زیبایی مطلقی هم باید وجود داشته باشد.

[ چهارشنبه 92/1/28 ] [ 6:37 صبح ] [ محمد رضا جبین پور ] [ نظرات () ]

گرایش های رشته ریاضی کاربردی

ریاضی کاربردی دارای گرایشهای زیر می باشد:

1-آنالیز عددی:
از دانشگاههای صاحب نام و دارای متخصص پیش کسوت در این رشته می توان
دانشگاه تربیت معلم تهران و یزد و سیستان و بلوچستان و تربیت مدرس ...را
نام برد. از پیش کسوت در این رشته می توان پروفسور اسماعیل بابلیان
و پروفسور عباس بندی و ...را نام برد.

2- تحقیق در عملیات: از
دانشگاههای صاحب نام در این رشته می توان دانشگاه تهران و تربیت معلم را
نام برد. متخصص در این رشته در ایران زیاد نمی باشد. از صاحب نظران این
رشته آقای دکتر جهانشاهلو را می توان نام برد.

3-نظریه گراف و ترکیبیات:
لازم به ذکر است که این گرایش در اغلب کشورهای خارجی زیر مجموعه ریاضی محض
محسوب می شود. در این گرایش دانشگاه صنعتی شریف و شهید بهشتی و صنعتی
اصفهان دارای مقطع دکتری هستند و با تربیت دانشجویان زبده در این مقطع
دانشگاههایی چون صنعتی امیرکبیر و مرکز تحقیقات علوم پایه زتجان این گرایش
را تدریس می نمایند. از بزرگان این رشته می توان پروفسور مهدی بهزاد
و پروفسور عبادا... محمودیان را نام برد. متخصص در این رشته نیز در ایران
کم می باشد.

4-معادلات دیفرانسیل (سیستم های دینامیکی):
از دانشگاههای دارای این گرایش در مقطع دکتری می توان دانشگاه علم و صنعت
ایران و صنعتی شریف و صنعتی اصفهان و تهران را نام برد. دانشگاههایی نظیر
شیراز و یزد و تبریز در مقطع ارشد این گرایش را دارند.

5-نظریه رمز - اطلاعات و کریپتوگرافی: متخصص در این رشته بسیار کم است و از دانشگاههایی که در مقطع دکتری این رشته را دارند دانشگاه صنعتی شریف و صنعتی اصفهان می باشد.

6- ریاضیات مالی: تحقیق
و تدریس در این رشته در ایران کم می باشد. اما مطمئنا در آینده جز رشته
های پرطرفدار محسوب خواهد گردید .در حال حاضر تا اونجا که من میدونم در
صنعتی اصفهان یه دانشجوی دکتری داره درس میخونه .

7- ریاضیات صنعتی:همانگونه
که از نام این رشته پیداست کاربرد ریاضی در علوم فنی بررسی می شود. در
ایران مقطع دکتری این رشته وجود ندارد اما دوره ارشد تدریس می شود.

8-بهینه سازی:
متخصص در این رشته کم است و از دانشگاههای دارای دکتری در این رشته
دانشگاه فردوسی مشهد و صنعتی اصفهان زیر نظر استاد ارجمند دکتر مرزبان می
باشد و دکتر وحیدیان کامیاد از سرآمدان این رشته است.

[ دوشنبه 92/1/26 ] [ 12:38 عصر ] [ محمد رضا جبین پور ] [ نظرات () ]

<< مطالب جدیدتر مطالب قدیمی‌تر >>

.: Weblog Themes By SibTheme :.

درباره وبلاگ